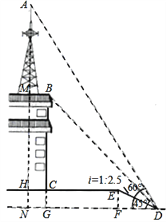
【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米。大家根据所学知识很快计算出了铁塔高AM。亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程。(数据![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
参考答案:
【答案】铁塔高AM约17米,过程见解析.
【解析】试题分析:根据坡度求出EF的长度,从而得出GD的长度,然后根据Rt△DBG的三角函数求出BG的长度,根据Rt△DAN的三角函数求出AN的长度,最后根据AM=AN-MN得出答案.
试题解析:∵斜坡的坡度是i= ![]() =
= ![]() ,EF=2, ∴FD=2.5 EF=2.5×2=5,
,EF=2, ∴FD=2.5 EF=2.5×2=5,
∵CE=13,CE=GF, ∴GD=GF+FD=CE+FD=13+5=18,
在Rt△DBG中,∠GDB=45°, ∴BG=GD=18,
在Rt△DAN中,∠NAD=60°,∴ND=NG+GD=CH+GD=2+18=20,
AN=NDtan60°=20×![]() =20
=20![]() , ∴AM=AN-MN=AN-BG=20
, ∴AM=AN-MN=AN-BG=20![]() -18≈17(米)
-18≈17(米)
答:铁塔高AM约17米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=
 ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )
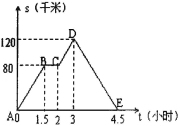
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,两条直线有两种位置关系,它们是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角为144°,那么这个角的余角是( )
A. 36° B. 44° C. 54° D. 126°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
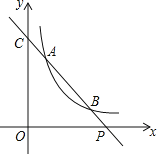
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
-
科目: 来源: 题型:
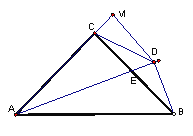
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=900,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD。下列结论:
①AC+CE=AB;②CD=
 ,③∠CDA=450 ,④
,③∠CDA=450 ,④ 为定值。
为定值。其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
相关试题

