【题目】如图,在□ABCD中,对角线AC,BD相交于点O,OA=5cm,E,F为直线BD上的两个动点(点E,F始终在□ABCD的外面),且DE=![]() OD,BF=
OD,BF=![]() OB,连接AE,CE,CF,AF.
OB,连接AE,CE,CF,AF.
(l)求证:四边形AFCE为平行四边形.
(2)若DE=![]() OD,BF=
OD,BF=![]() OB,上述结论还成立吗?由此你能得出什么结论?
OB,上述结论还成立吗?由此你能得出什么结论?
(3)若CA平分∠BCD,∠AEC=60°,求四边形AECF的周长.

参考答案:
【答案】见解析
【解析】(1)由平行四边形的性质可知OA=OC、OB=OD,结合BF=![]() OD、BF=
OD、BF=![]() OB可得出OE=OF,根据“对角线互相平分的四边形是平行四边形”即可证出四边形AFCE为平行四边形;
OB可得出OE=OF,根据“对角线互相平分的四边形是平行四边形”即可证出四边形AFCE为平行四边形;
(2)由DE=![]() OD、BF=
OD、BF=![]() OB可以得出OE=OF,根据“对角线互相平分的四边形是平行四边形”即可证出四边形AFCE为平行四边形,由此可得出原结论成立。再找出结论“DE=
OB可以得出OE=OF,根据“对角线互相平分的四边形是平行四边形”即可证出四边形AFCE为平行四边形,由此可得出原结论成立。再找出结论“DE=![]() OD,BF=
OD,BF=![]() OB,则四边形AFCE为平行四边形”即可;
OB,则四边形AFCE为平行四边形”即可;
(3)根据平行四边形的性质结合CA平分∠BCD,即可得出AD=CD,进而可得出OE是AC的垂直平分线,再根据∠AEC=60°可得出△ACE是等边三角形,根据OA的长度即可得出AE、CE的长度,套用平行四边形周长公式即可求出四边形AECF的周长.
解:(1)∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵DE=![]() OD,BF=
OD,BF=![]() OB,∴DE=BF.∴DE=OF,
OB,∴DE=BF.∴DE=OF,
∴四边形AFCE为平行四边形.
(2)成立.结论:若DE=![]() OD,BF=
OD,BF=![]() OB,则四边形AFCE为平行四边形.
OB,则四边形AFCE为平行四边形.
(3)在□ABCD中,AD//BC,∴∠DAC=∠ACB.
∵CA平分∠BCD,∠ACB=∠ACD.
∴∠ACD=∠DAC,
∴AD=CD,
∵OA=OC,∴OE⊥AC,
∴OE是AC的垂直平分线,
∴AE=CE,
∵∠AEC=60°,△ACE是等边三角形,
∴AE=CE=AC=2OA=10cm,
在□AECF中,AF=CE,AE=CF,∴四边形AECF的周长为2(10+10)=40(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种生物细胞的直径约为0.000056米,用科学记数法表示为米.
-
科目: 来源: 题型:
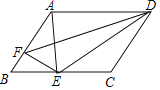
查看答案和解析>>【题目】如图,点E为□ABCD的边BC上一点,线段AE的垂直平分线恰好经过点D且交AB于点F,△BEF和△CDE的周长分别为8和13,则□ABCD的周长为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“”表示一种新运算,它的意义是ab=ab-(a+b)
(1)求(-2)(-3);
(2)求(34)(-5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】立方根等于本身的数是( )
A.-1B.0C.±1D.±1或0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列具有相反意义的量是( )
A. 向西走 2 米与向南走 3 米 B. 胜 2 局与负 3 局
C. 增加2厘米和减少2千克 D. 盈利 3 万元与支出 3 万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7B.5,12,13C.1,4,9D.5,11,12
相关试题

