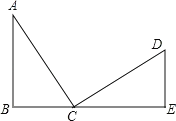
【题目】如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=________.
参考答案:
【答案】a+b
【解析】由直角三角形的性质求出∠DCE=∠A,由AAS证明△ABC≌△CED,得出对应边相等BC=DE=b,CE=AB=a,即可得出结果.
解:∵∠E=90°,∠D=60°,
∴∠DCE=90°-60°=30°=∠A,
在△ABC和△CED中,∠B=∠E=90°,∠A=∠DCE,AC=CD,
∴△ABC≌△CED(AAS)
∴BC=DE=b,CE=AB=a,
∴BE=BC+CE=a+b.
故答案为:a+b.
“点睛”本题考查了全等三角形的判定与性质、直角三角形的性质;证明三角形全等得出对应边相等是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“在同一平面内,垂直于同一直线的两直线互相平行”改写成“如果……,那么……”
的形式:
-
科目: 来源: 题型:
查看答案和解析>>【题目】武汉某天的最高气温是7℃最低气温是-3℃,那么当天的温差是( )℃
A. 4 B. 10 C. -10 D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一个平面内,不重合的两条直线的位置关系可能是 ( )
A. 相交或平行 B. 相交或垂直 C. 平行或垂直 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学活动课上,将边长为
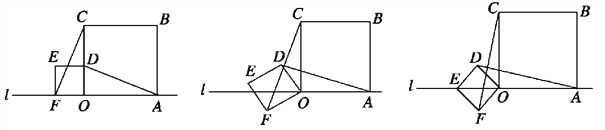
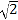 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个外角都是72°,则这个多边形是( )
A.正方形B.正五边形C.正六方形D.正七边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 P(1, 2) 关于 y 轴对称的点的坐标是_____.
相关试题

