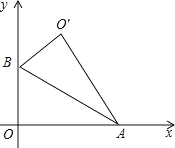
【题目】(2016宁夏第14题)如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
参考答案:
【答案】(![]() ,
,![]() )
)
【解析】
试题分析:作O′C⊥y轴于点C,首先根据点A,B的坐标分别为(![]() ,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=
,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=![]() x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
∵点A,B的坐标分别为(![]() ,0),(0,1),∴OB=1,OA=
,0),(0,1),∴OB=1,OA=![]() ,∴tan∠BAO=
,∴tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=30°,∴∠OBA=60°,∵Rt△AOB沿着AB对折得到Rt△AO′B,∴∠CBO′=60°,
∴设BC=x,则OC′=![]() x,∴x2+(
x,∴x2+(![]() x)2=1,解得:x=
x)2=1,解得:x=![]() (负值舍去),
(负值舍去),
∴OC=OB+BC=1+![]() =
=![]() ,∴点O′的坐标为(
,∴点O′的坐标为(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】把实数0.45精确到0.1的近似值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)
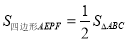 ;(4)EF=AP.上述结论中始终正确的结论有( )
;(4)EF=AP.上述结论中始终正确的结论有( )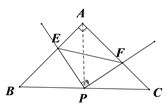
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC与△DEF相似且周长比为2:5,则△ABC与△DEF的相似比为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△BDE均为等边三角形,AB<BD,若△ABC不动,将△BDE绕点B旋转则在旋转过程中,AE与CD的大小关系为( )
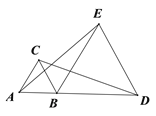
A. AE=CD B. AE>CD C. AE<CD D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:
金额/元
5
6
7
10
人数
2
3
2
1
这8名同学捐款的平均金额为( )
A.3.5元
B.6元
C.6.5元
D.7元 -
科目: 来源: 题型:
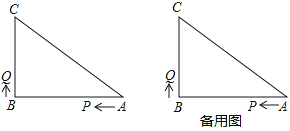
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90 ,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求线段PQ的长?
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB是等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间?
相关试题

