搜索
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E
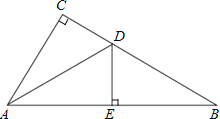
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
参考答案：
【答案】（1）见解析（2）BD=2
【解析】解：（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴CD=ED，∠DEA=∠C=90°。
∵在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL）。
（2）∵Rt△ACD≌Rt△AED ，CD=1，∴DC=DE=1。
∵DE⊥AB，∴∠DEB=90°。
∵∠B=30°，∴BD=2DE=2。
（1）根据角平分线性质求出CD=DE，根据HL定理求出另三角形全等即可。
（2）求出∠DEB=90°，DE=1，根据含30度角的直角三角形性质求出即可。
-
科目： 来源： 题型：
查看答案和解析>>【题目】两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．
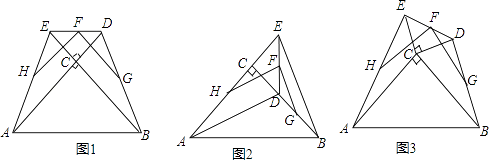
（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为和位置关系为；
（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；
（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，六边形ABCDEF的六个内角都相等．若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于_________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B、E分别在直线AC和DF上，若∠AGB=∠EHF，∠C=∠D，可以证明∠A=∠F．请完成下面证明过程中的各项“填空”．
证明：∵∠AGB=∠EHF（理由： ）
∠AGB= （对顶角相等）
∴∠EHF=∠DGF，∴DB∥EC（理由： ）
∴ =∠DBA（两直线平行，同位角相等）
又∵∠C=∠D，∴∠DBA=∠D，
∴DF∥ （内错角相等，两直线平行）
∴∠A=∠F（理由： ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某县为创建省文明卫生城市，计划将城市道路两旁的人行道进行改造，经调查可知，若该工程由甲工程队单独来做恰好在规定时间内完成；若该工程由乙工程队单独完成，则需要的天数是规定时间的2倍，若甲、乙两工程队合作6天后，余下的工程由甲工程队单独来做还需3天完成．
（1）问该县要求完成这项工程规定的时间是多少天？
（2）已知甲工程队做一天需付给工资5万元，乙工程队做一天需付给工资3万元．现该工程由甲、乙两个工程队合作完成，该县准备了工程工资款65万元．请问该县准备的工程工资款是否够用？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）
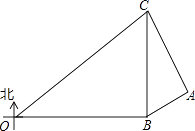
（1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？
（2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？
（3）若敌舰A沿最短距离的路线以20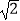
海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？ -
科目： 来源： 题型：
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1)，然后将剩余部分拼成一个长方形(如图2).
(1)探究：上述操作能验证的等式是 ；(请选择正确的一个)
A．a2-2ab+b2=(a-b)2 B．a2-b2=(a+b)(a-b)
C．a2+ab=a(a+b)
(2)应用：利用你从(1)选出的等式，完成下列各题：
①已知9x2-4y2=24，3x+2y=6，求3x-2y的值；
②计算：
相关试题
