【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
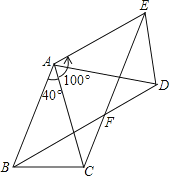
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形
参考答案:
【答案】(1)证明见解析;(2)40°;(3)证明见解析.
【解析】
试题分析:(1)根据旋转角求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等.
(2)根据全等三角形对应角相等,得出∠ACE=∠ABD,即可求得.
(3)根据对角相等的四边形是平行四边形,可证得四边形ABFE是平行四边形,然后依据邻边相等的平行四边形是菱形,即可证得.
试题解析:(1)∵△ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD与△ACE中

∴△ABD≌△ACE(SAS).
(2)∵∠CAE=100°,AC=AE,
∴∠ACE=![]() (180°-∠CAE)=
(180°-∠CAE)=![]() (180°-100°)=40°;
(180°-100°)=40°;
(3)∵∠BAD=∠CAE=100°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°-∠BAE-∠ABD-∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴平行四边形ABFE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=kx+b的图象经过点P(﹣2,3),则2k﹣b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=(k﹣1)x|k|+b+1是正比例函数,则k和b的值为( )
A.k=±1,b=﹣1
B.k=±1,b=0
C.k=1,b=﹣1
D.k=﹣1,b=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知1是关于x的一元二次方程x2+mx+n=0的一个根,那么m+n=________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
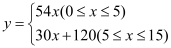
(1)李明第几天生产的粽子数量为420只?
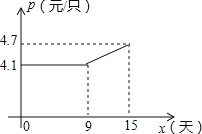
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】钟表在12时15分时刻的时针与分针所成的角是_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A. -a不一定是负数 B. |a|是一个正数
C. 若|a|=a,则a>0;若|a|=-a,则a<0 D. 只有负数的绝对值是它的相反数
相关试题

