【题目】已知方程x2+2kx+k2-2k+1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若![]() =4,求k的值.
=4,求k的值.
参考答案:
【答案】(1) k≥![]() ;(2) k=1.
;(2) k=1.
【解析】分析:(1)根据方程有两个实数根,可得△≥0可求出k的范围;(2)根据根与系数的关系得出:![]() ,把原式变形后代入,即可求解.
,把原式变形后代入,即可求解.
本题解析:∵关于x的一元二次方程![]() ,有两个不相等的实数根,
,有两个不相等的实数根,
∴![]() ,解得;k≥
,解得;k≥![]() ,
,
∴实数k的取值范围是:k≥![]() .
.
(2) ∵![]() ,
,![]() ,
,
∴ ![]()
∴![]() , ∴
, ∴![]() ∵k≥
∵k≥![]() ,∴k=1.
,∴k=1.
点睛:本题考查了一元二次方程ax+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;△<0时,方程没有实数根,以及利用根与系数的关系求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A,B,O,C为数轴上四点,点A对应数a(a<﹣2),点O对应0,点C对应3,AB=2 (AB表示点A到点B的距离).
(1)填空:点C到原点O的距离 ,:点B对应的数 .(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若BC=5,求a的值和点A在刻度尺上对应的刻度.
(3)如图3,在(2)的条件下,点A以1单位长度/秒的逮度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点D的距离相等,求点C的运动速度.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,线段AC=8,BC=6,点M、N分别是AC、BC的中点.
(1)求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,你能猜想出MN的长度吗?请说明理由.
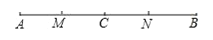
-
科目: 来源: 题型:
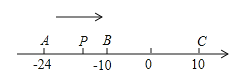
查看答案和解析>>【题目】已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:PA= ,PC= .
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在运动过程中,t为何值时P与Q重合?
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的两边分别平行于另一个角的两边,且其中一个角是55°,则另一个角的度数为 ______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
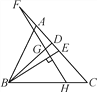
A. ①②③ B. ①②④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.必然事件发生的概率是0
B.“任意画一个等边三角形,其内角和是180°”是随机事件
C.投一枚图钉,“钉尖朝上”的概率不能用列举法求得
D.如果明天降水的概率是50%,那么明天有半天都在下雨
相关试题

