搜索
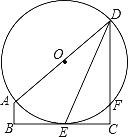
【题目】如图，在直角梯形ABCD中，AB∥CD，∠C＝90°，以AD为直径的⊙O与BC相切于点E，交CD于点F，连接DE．
（1）证明：DE平分∠ADC；
（2）已知AD＝4，设CD的长为x（2＜x＜4）．
①当x＝2.5时，求弦DE的长度；
②当x为何值时，DFFC的值最大？最大值是多少？
【答案】（1）见解析；（2）①
；②x＝3时，DFCF的值最大，最大值为2
【解析】
（1）连接OE，根据已知可推出AB∥OE∥CD，可得∠OED＝∠CDE，再根据OD＝OE，可得∠OED＝∠ODE，即可证明；
（2）①连接AF交OE于H，由现有条件可推出AB＝1.5，然后可证四边形ABCF是矩形，可得AH＝FH，AB＝CF＝HE＝1.5，OH＝OE﹣EH＝0.5，可得AH＝
=
=
，根据勾股定理即可得出答案；
②设AB＝CF＝m，根据OE＝
（AB+CD），可得x+m＝4，即可得DFCF的函数表达式，根据函数的性质即可得出答案．
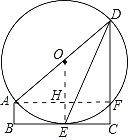
（1）证明：如图，连接OE，
∵BC是⊙O的切线，
∴OE⊥BC，
∵AB∥CD，∠C＝90°，
∴∠B＝90°，
∴AB⊥BC，CD⊥BC，
∴AB∥OE∥CD，
∴∠OED＝∠CDE，
∵OD＝OE，
∴∠OED＝∠ODE，
∴∠ODE＝∠CDE，
∴ED平分∠ADC；
（2）①连接AF交OE于H，
∵AB∥OE∥CD，AO＝OD，
∴BE＝EC，
∴OE＝（AB+CD），
∵OE＝2，CD＝2.5，
∴AB＝1.5，
∵AD是⊙O的直径，
∴∠AFD＝90°，
∵∠B＝∠C＝9°，
∴四边形ABCF是矩形，
∴AF∥BC，
∵OE⊥BC，
∴OE⊥AF，
∴AH＝FH，AB＝CF＝HE＝1.5，
∴OH＝OE﹣EH＝0.5，
∴AH＝==，
∴AH＝FH＝CE＝，
∴DE＝
＝
＝；
②设AB＝CF＝m，
∵OE＝（AB+CD），
∴x+m＝4，
∴m＝4﹣x，
∴DFCF＝（（4﹣x）（2x﹣4）＝﹣2x2+12x﹣16＝﹣2（x﹣3）2+2，
∵﹣2＜0，
∴x＝3时，DFCF的值最大，最大值为2．
