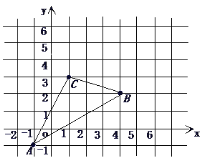
【题目】△ABC在直角坐标系中的位置如图所示,
(1)请你写出△ABC各点的坐标,
(2)求出S△ABC的面积,
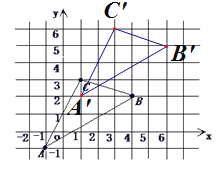
(3)若把△ABC向上平移3个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标.
参考答案:
【答案】(1)A(﹣1,-1)、B(4,2)C(1,3);(2)7;(3)A′、(1,2)B′、(6,5)C′(3,6)
【解析】(1)根据各点所在象限的符号和距坐标轴的距离可得各点的坐标;
(2)观察图形,可知△ABC的面积可视为边长为4,5的长方形的面积与直角边长为2、4的直角三角形,直角边长为3、5的直角三角形及边长为1,3的直角三角形面积和的差,利用直角三角形面积公式及长方形面积公式进行计算,即可使(2)得解;
(3)把三角形ABC的各顶点向上平移2个单位,再向右平移2个单位得到平移后的三个点,顺次连接平移后的各顶点即为平移后的三角形,根据各点所在象限的符号和距坐标轴的距离可得各点的坐标.
(1)A(﹣1,-1)、B(4,2)C(1,3),
(2)S△ABC=4×5-![]() ×5×3-
×5×3-![]() ×3×1-
×3×1-![]() ×4×2=7,
×4×2=7,
(3)A′、(1,2)B′、(6,5)C′(3,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.
(1)求证:M与其“友谊数”的差能被15整除;
(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
-
科目: 来源: 题型:
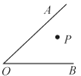
查看答案和解析>>【题目】如图,P为∠AOB内一定点,M,N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2﹣
x2﹣  x+
x+  与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,已知点D(0,﹣
与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,已知点D(0,﹣  ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM,NQ,求PM+MN+NQ的最小值;
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△BPQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E.则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒1cm,设出发的时间为t秒.问t为何值时,△BCP为等腰三角形?

-
科目: 来源: 题型:
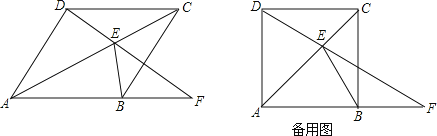
查看答案和解析>>【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
相关试题

