Question

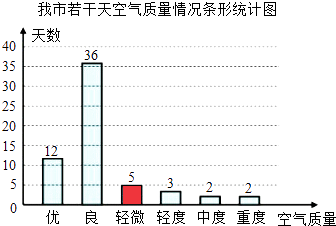
【题目】为了解我市的空气质量情况，某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．
请你根据图中提供的信息，解答下列问题：
（1）计算被抽取的天数；
（2）请补全条形统计图，并求扇形统计图中表示“优”的扇形的圆心角度数；
（3）请估计该市这一年（365天）达到“优”和“良”的总天数．

Answer 1

【答案】
（1）解：扇形图中空气为优所占比例为20%，条形图中空气为优的天数为12天，

∴被抽取的总天数为：12÷20%=60（天）

（2）解：轻微污染天数是60﹣36﹣12﹣3﹣2﹣2=5天；

表示优的圆心角度数是 360°=72°，

如图所示：

（3）解：样本中优和良的天数分别为：12，36，

一年（365天）达到优和良的总天数为： ×365=292（天）．

故估计本市一年达到优和良的总天数为292天

【解析】（1）根据扇形图中空气为优所占比例为20%，条形图中空气为优的天数为12天，即可得出被抽取的总天数；（2）轻微污染天数是60﹣36﹣12﹣3﹣2﹣2=5天；利用360°乘以优所占的份额即可得优的扇形的圆心角度数；（3）利用样本中优和良的天数所占比例乘以一年（365天）即可求出达到优和良的总天数．