【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
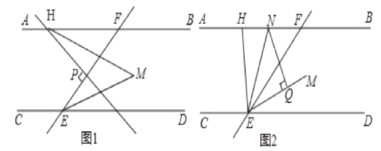
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
参考答案:
【答案】(1)45o (2)∠FHE=2∠ENQ或∠FHE=180°2∠ENQ,证明见解析
【解析】
(1)首先作MQ∥AB,根据平行线的性质,推得∠M=![]() (∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(2)①如图2,首先判断出∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
②如图3,首先判断出∠NEQ=∠QEF-∠NEF=![]() (∠DEF-∠HEF)=
(∠DEF-∠HEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
如图1,作MQ∥AB,
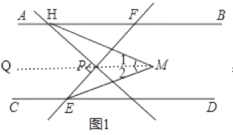
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=![]() (∠FHP+∠FED)=
(∠FHP+∠FED)= ![]() (∠FHP+∠HFP),
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°90°=90°,
∵∠1+∠2=∠M,
∴∠M=![]() ×90°=45°.
×90°=45°.
(2)①如图2,
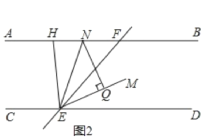
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,
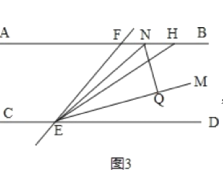
∠FHE=180°2∠ENQ,理由如下:
∠NEQ=∠QEF∠NEF=![]() (∠DEF∠HEF)=
(∠DEF∠HEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=180°∠CEH=180°2∠ENQ.
综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t
频数
百分比
10≤t<30
4
8%
30≤t<50
8
16%
50≤t<70
a
40%
70≤t<90
16
b
90≤t<110
2
4%
合计
50
100%
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?
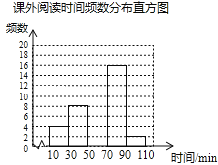
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,BE⊥CD于点E,点F在AB上,且AF=CE,连接DF.
(1)求证:四边形BEDF是矩形;
(2)连接CF,若CF平分∠BCD,且CE=3,BE=4,求矩形BEDF的面积.
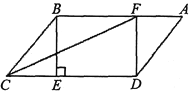
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
(1)在正方形网格中,作出△AB1C1;
(2)设网格小正方形的边长为1,求旋转过程中动点B所经过的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为
 .
.(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
相关试题

