搜索
【题目】如图，△ABC≌△ADE，且∠CAD＝10°，∠B＝∠D＝25°，∠EAB＝120°，试求∠DFB和∠DGB的度数．
参考答案：
【答案】90°；65°
【解析】试题分析：由△ABC≌△ADE，可得∠DAE=∠BAC=
（∠EAB-∠CAD），根据三角形外角性质可得∠DFB=∠FAB+∠B，因为∠FAB=∠FAC+∠CAB，即可求得∠DFB的度数；根据三角形内角和定理可得∠DGB=∠DFB-∠D，即可得∠DGB的度数．
试题解析：∵△ABC≌△ADE，
∴∠DAE=∠BAC=
（∠EAB-∠CAD）=
（120°-10°）=55°．
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB-∠D=90°-25°=65°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】合肥百大集团新进了40台空调机，60台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：
空调机
电冰箱
甲连锁店
200
170
乙连锁店
160
150
设集团调配给甲连锁店x台空调机，集团卖出这100台电器的总利润为y（元）．
（1）求y关于x的函数关系式，并求出x的取值范围；
（2）为了促销，集团决定仅对甲连锁店的空调机每台让利a元销售，其他的销售利润不变，并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润，问该集团应该如何设计调配方案，才能使总利润达到最大？
-
科目： 来源： 题型：
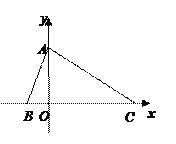
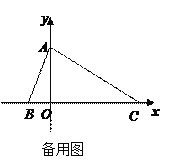
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（0，2）、（－1，0）、（4，0）．P是线段BC上的一动点（点P与点B、C不重合），假设p的横坐标是t.过点P的直线与直线y＝x平行且与AC相交于点Q．设△QPC关于直线PQ的对称的图形与四边形ABPQ重叠部分的面积为S．
⑴点C关于直线PQ的对称点C′的坐标为________；
⑵△ABC是什么三角形？为什么？
（3）求S与t的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：
信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；
信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．
根据以上信息，原来报名参加的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】要对一块长60米，宽40米的矩形荒地ABCD进行绿化和硬化、设计方案如图所示，矩形P、Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽都相等，并使两块绿地面积的和为矩形ABCD面积的
，求P、Q两块绿地周围的硬化路面的宽．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列选项中，显示部分在总体中所占百分比的统计图是（ ）
A.扇形图
B.条形图
C.折线图
D.直方图 -
科目： 来源： 题型：
查看答案和解析>>【题目】计算aa﹣1的结果为（ ）
A.﹣1
B.0
C.1
D.-a
相关试题
