【题目】如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF. 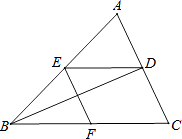
参考答案:
【答案】证明:∵ED∥BC,EF∥AC, ∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
∴EB=CF.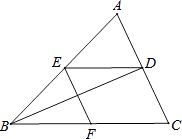
【解析】本题考查平行四边形的判定和性质、等腰三角形的判定和性质等知识,先利用平行四边形性质证明DE=CF,再证明EB=ED,即可解决问题.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin30°+3﹣1+(
 ﹣1)0﹣
﹣1)0﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表
优秀
良好
合格
不合格
七年级
a
20
24
8
八年级
29
13
13
5
九年级
24
b
14
7
根据以上信息解决下列问题:

(1)在统计表中,a的值为 , b的值为;
(2)在扇形统计图中,八年级所对应的扇形圆心角为度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.
(1)若先从袋子中拿走m个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则m的值为;
(2)若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:
 ≈1.73)
≈1.73) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.

(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
相关试题

