【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10, 求四边形ABCD的面积.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)108
【解析】试题分析:(1)、根据正方形的性质以及BE=DF得出△CBE和△CDF全等,从而得出答案;(2)、延长AD至F,使DF=BE.连接CF,然后证明△ECG和△FCG全等,从而得出GE=GF,从而得出答案;(3)、过C作CG⊥AD,交AD延长线于G,根据(1)(2)得出DG=6,设AB=x,则AE=x-4,AD=x-6,根据Rt△AED的勾股定理求出x的值,最后根据四边形的面积= ![]() 得出答案.
得出答案.
试题解析:(1)证明:在正方形ABCD中, ∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF. ∴CE=CF.
(2)证明: 如图2,延长AD至F,使DF=BE.连接CF.
由(1)知△CBE≌△CDF, ∴∠BCE=∠DCF. ∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°, 又∠GCE=45°,∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC, ∴△ECG≌△FCG. ∴GE=GF
∴GE=DF+GD=BE+GD.
(3)解:如图3,过C作CG⊥AD,交AD延长线于G.
在四边形ABCD中, ∵AD∥BC,∴∠A=∠B=90°, 又∠CGA=90°,AB=BC,
∴四边形ABCD 为正方形. ∴AG=BC. 已知∠DCE=45°,
根据(1)(2)可知,ED=BE+DG. 所以10=4+DG,即DG=6.
设AB=x,则AE=x-4,AD=x-6
在Rt△AED中, ∵![]() ,即
,即![]() .
.
解这个方程,得:x=12,或x=-2(舍去). ∴AB=12.
所以四边形ABCD的面积为S=![]()
答:四边形ABCD的面积为108.


-
科目: 来源: 题型:
查看答案和解析>>【题目】22(﹣2)3=;(
 )0×3﹣2=;(﹣0.25)2013×42014= .
)0×3﹣2=;(﹣0.25)2013×42014= . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算。
(1)若28n16n=222 , 求n的值.
(2)已知3m=6,9n=2,求32m﹣4n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明坐于堤边垂钓,如图,河堤
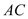 的坡角为
的坡角为 ,
,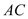 长为
长为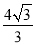 米,钓竿
米,钓竿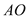 的倾斜角是
的倾斜角是 ,其长为
,其长为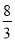 米,若
米,若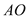 与钓鱼线
与钓鱼线 的夹角为
的夹角为 ,求浮漂
,求浮漂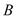 与河堤下端
与河堤下端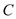 之间的距离.
之间的距离.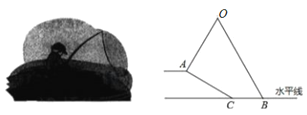
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有2400名学生,估计全校最喜爱文学类图书的学生有多少人?
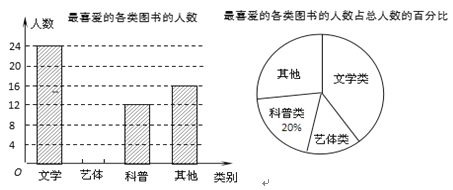
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. (﹣a2)3=a6B. a2a3=a6C. (﹣ab)2=a2bD. 2a6÷a3=2a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果水位升高3m时水位变化记作+3m,那么水位下降2m时水位变化记作:m.
相关试题

