【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.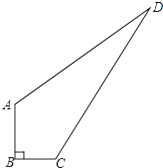
参考答案:
【答案】解:连结AC, 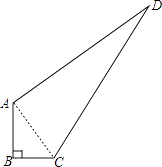
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC= ![]() =5(m),
=5(m),
S△ABC= ![]() ×3×4=6(m2),
×3×4=6(m2),
在△ACD中,
∵AD=12m,AC=5m,CD=13m,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD= ![]() ×5×12=30(m2).
×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
【解析】抓住已知条件∠B=90°,因此连接AC,构造直角三角形,将要所求的问题转化到直角三角形中求解。利用勾股定理及逆定理即可求得这块草地的面积。
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适宜采用普查方式的是( )
A. 对量子科学通信卫星上某种零部件的调查B. 对我国初中学生视力状况的调查
C. 对一批节能灯管使用寿命的调查D. 对“最强大脑”节目收视率的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
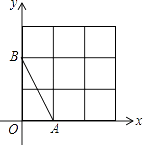
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,∠AOB=60°,∠BOC=45°,则∠AOC=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在显微镜下,人体内一种细胞的形状可以近似地看成圆,它的直径约为0.00000156米,用科学记数法表示为米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,
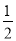 ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组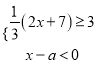 无解,且使关于x的分式方程
无解,且使关于x的分式方程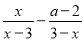 =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )A. ﹣2 B. ﹣3 C. -
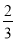 D.
D. 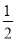
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A. 任何数都有平方根 B. 只有正数才有平方根
C. 负数没有立方根 D. 存在算术平方根等于本身的数
相关试题

