【题目】为进一步推进青少年毒品预防教育“6.27”过程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,我市高度重视全国青少年禁毒知识竞赛活动,针对某校七年级学生的知识竞赛成绩绘制了如下不完整的统计图表.

据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请求出C组所在扇形统计图中的圆心角的度数;
(3)补全知识竞赛成绩频数分布直方图;
(4)已知我市七年级有180000名学生,请估算全市七年级知识竞赛成绩低于80分的人数.
参考答案:
【答案】(1)300;50(2)54°(3)见解析(4)9000人
【解析】
(1)根据D组人数以及百分比求出总人数,再求出a,b即可.
(2)根据圆心角=360°×百分比,计算即可.
(3)根据B,E两组人数画出直方图即可.
(4)利用样本估计总体的思想解决问题即可.
(1)∵被调查的总人数为200÷20%=1000(人),
∴a=1000×![]() =300,b=1000(300+300+150+200)=50.
=300,b=1000(300+300+150+200)=50.
故答案为300,50.
(2)C组所在扇形统计图中的圆心角的度数为360°×![]() =54°;
=54°;
(3)补全统计图如下:
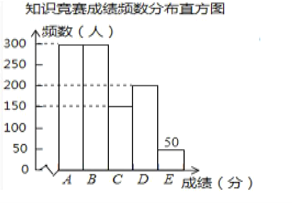
(4)全市九年级知识竞赛成绩低于80分人数约为180000×![]() =9000人.
=9000人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 在直角坐标系第一象限内,
在直角坐标系第一象限内, 与
与 轴重合,
轴重合, ,
,
 ,
, ,点
,点 从点
从点 出发,以每秒
出发,以每秒 个单位向点
个单位向点 运动,点
运动,点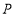 同时从点
同时从点 出发以每秒3个单位向点
出发以每秒3个单位向点 运动,当其中有一点到达终点时,另一点立即停止运动.
运动,当其中有一点到达终点时,另一点立即停止运动. 是射线
是射线 上的一点,且
上的一点,且 ,以
,以 为邻边作矩形
为邻边作矩形 .设运动时间为
.设运动时间为 秒.
秒.
(1)写出点
 的坐标( , );
的坐标( , ); ;
; .(用
.(用 的代数式表示)
的代数式表示)(2)当点
 落在
落在 上时,求此时
上时,求此时 的长?
的长?(3)①在
 的运动过程中,直角坐标系中是否存在点
的运动过程中,直角坐标系中是否存在点 ,使得
,使得 四点构成的四边形是菱形?若存在求出
四点构成的四边形是菱形?若存在求出 的值,不存在,请说明理由.
的值,不存在,请说明理由.②如图2,以
 为边按逆时针方向做正方形
为边按逆时针方向做正方形 ,当正方形
,当正方形 的顶点
的顶点 或
或 落在矩形
落在矩形 的某一边上时,则
的某一边上时,则 (直接写出答案).
(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的结论有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.

试说明:AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD.当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?直接写出结论,其数量关系为 .

相关试题

