【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究,以下是探究发现运用过程,请补充完整.
(1)操作发现
在作函数y=|x|的图象时,采用了分段函数的办法,该函数转化为y=![]() ,请在如图1所示的平面直角坐标系中作出函数的图象;
,请在如图1所示的平面直角坐标系中作出函数的图象;
(2)类比探究
作函数y=|x-1|的图象,可以转化为分段函数y=![]() ,然后分别作出两段函数的图象.聪明的小昕利用坐标平面上的轴对称知识,把函数y=x-1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x-1|的图象,如图2所示;
,然后分别作出两段函数的图象.聪明的小昕利用坐标平面上的轴对称知识,把函数y=x-1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x-1|的图象,如图2所示;
(3)拓展提高
如图3是函数y=x2-2x-3的图象,请在原平面直角坐标系作函数y=|x2-2x-3|的图象;
(4)实际运用
①函数y=|x2-2x-3|的图象与x轴有 个交点,对应方程|x2-2x-3|=0有 个实根;
②函数y=|x2-2x-3|的图象与直线y=5有 个交点,对应方程|x2-2x-3|=5有 个实根;
③函数y=|x2-2x-3|的图象与直线y=4有 个交点,对应方程|x2-2x-3|=4有 个实根;
④关于x的方程|x2-2x-3|=a有4个实根时,a的取值范围是 .

参考答案:
【答案】(1)作图见解析; (3) 作图见解析;
(4)①2,2;②2,2;③3,3;④0<a<4.
【解析】试题分析: ![]() 利用描点法画
利用描点法画![]() 的图象;
的图象;
![]() 根据绝对值的意义,利用分类讨论的思想写出分段函数;
根据绝对值的意义,利用分类讨论的思想写出分段函数;
![]() 与
与![]() 画函数图象的方法一样,把函数
画函数图象的方法一样,把函数![]() 的图象在
的图象在![]() 轴下面部分,沿
轴下面部分,沿![]() 轴进行翻折可得到函数
轴进行翻折可得到函数![]() 的图象;
的图象;
![]() 利用画函数图象,通过确定
利用画函数图象,通过确定![]() 的图象与直线
的图象与直线![]() 的交点个数解决问题.
的交点个数解决问题.
试题解析: ![]() 操作发现如图
操作发现如图![]() ,
,
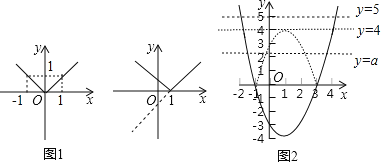
![]() 类比探究
类比探究
作函数![]() 的图象,可以转化为分段函数
的图象,可以转化为分段函数![]()
![]() 拓展提高
拓展提高
把函数![]() 的图象在
的图象在![]() 轴下面部分,沿
轴下面部分,沿![]() 轴进行翻折可得到函数的图象;
轴进行翻折可得到函数的图象;
与![]() 轴上及上面部分组成了函数
轴上及上面部分组成了函数![]() 的图象,如图
的图象,如图![]() ;
;
![]() ①函数
①函数![]() 的图象与
的图象与![]() 轴有
轴有![]() 个交点,对应方程
个交点,对应方程![]() 有
有![]() 个实根;
个实根;
②函数![]() 的图象与直线
的图象与直线![]() 有
有![]() 个交点,对应方程
个交点,对应方程![]() 有
有![]() 个实根;
个实根;
③函数![]() 的图象与直线
的图象与直线![]() 有
有![]() 个交点,对应方程
个交点,对应方程![]() 有
有![]() 个实根;
个实根;
④关于![]() 的方程
的方程![]() 有
有![]() 个实根时,
个实根时, ![]() 的取值范围是
的取值范围是![]()
故答案为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2互补,∠1=26°30′,则∠2的度数为( )
A. 153°30′B. 163°30′C. 173°30′D. 183°30′
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>0,b<0,则b,b+a,b﹣a中最大的一个数是( )
A.a
B.b+a
C.b﹣a
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】将6.18×10-3化为小数的是( )
A. 0.000618 B. 0.00618 C. 0.0618 D. 0.618
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品原价是121元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5cm,A是线段OP的中点,当OP=7cm时,点A与⊙O的位置关系是( )
A. 点A在⊙O内B. 点A在⊙O上C. 点A在⊙O外D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.

(1)求该抛物线的表达式及其顶点C的坐标;
(2)若点M是抛物线上的一个动点,且位于第一象限内.
①设△ABM的面积为S,试求S的最大值;
②若S为整数,则这样的M点有 个.
相关试题

