Question

【题目】如图，已知：△ABC内接于⊙O，点D在OC的延长线上，sinB=，∠D=30度．

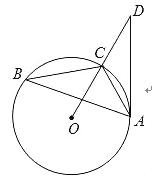
（1）求证：AD是⊙O的切线；

（2）若AC=6，求AD的长．

Answer 1

【答案】（1）AD是⊙O的切线；（2）

【解析】

试题分析：（1）要证明AD是⊙O的切线，只要证明∠OAD=90°即可；

（2）根据已知可得△AOC是等边三角形，从而得到OA=AC=6，则可以利用勾股定理求得AD的长．

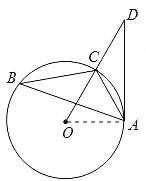
试题解析：（1）证明：如图，连接OA；

∵sinB=，

∴∠B=30°，

∵∠AOC=2∠B，

∴∠AOC=60°；

∵∠D=30°，

∴∠OAD=180°﹣∠D﹣∠AOD=90°，

∴AD是⊙O的切线．

（2）解：∵OA=OC，∠AOC=60°，

∴△AOC是等边三角形，

∴OA=AC=6，

∵∠OAD=90°，∠D=30°，

∴AD=AO=．