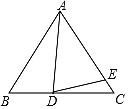
【题目】如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
参考答案:
【答案】(1)20°,10°;(2)结论:α=2β,理由见解析.
【解析】
(1)根据∠BAD=∠BAC-∠DAE,∠AED=∠CDE+∠C,进行计算即可解决问题;
(2)α=2β,理由是:设∠BAC=x°,∠DAE=y°,则α=x°-y°,同理求出∠ACB=![]() 和∠AED=
和∠AED=![]() ,利用外角定理得:β=∠AED-∠ACB,代入可得结论.
,利用外角定理得:β=∠AED-∠ACB,代入可得结论.
(1)∵AB=AC,
∴∠B=∠C=60°,
∴∠BAC=60°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠DAE=40°,
∴∠BAD=∠BAC-∠DAE=20°,
∵∠AED=∠CDE+∠C,
∴∠CDE=70°-60°=10°.
(2)结论:α=2β,理由是:
设∠BAC=x°,∠DAE=y°,则α=x°-y°,
∵∠ACB=∠ABC,
∴∠ACB=![]() ,
,
∵∠ADE=∠AED,
∴∠AED=![]() ,
,
∴β=∠AED-∠ACB=![]() -
-![]() =
=![]() =
=![]() ,
,
∴α=2β;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2012~2016年常住人口数统计如图所示。
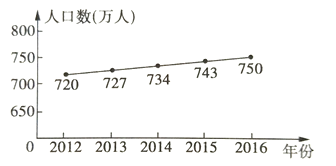
(1)该市常住人口数2016年比2015年增加了___________万人;
(2)与上一年相比,该市常住人口数增长率最大的年份是__________________;
(3)预测2017年该市常住人口大约有多少万人,并用所学的统计知识说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表。
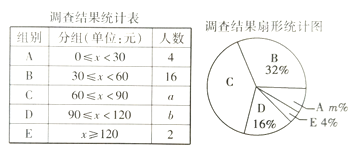
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有_____________人,a+b=______________,m=________;
(2)求扇形统计图中扇形C的圆心角度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事,引起社会的广泛关注和讨论,明德集团某校文学社就此召开了一次研讨会,为了传承中国传统文化,并组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:

组别
正确字数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
n
根据以上信息完成下列问题:
(1)求统计表中的m,n,并补全条形统计图;
(2)扇形统计图中“C组“所对应的圆心角的度数是多少;
(3)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生的特长爱好,提髙学生的综合素质,某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买2个竖笛和1个尤克里里共需290元;竖笛单价比尤克里里单价的一半少25元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共20个,但要求购买竖笛和尤克里里的总费用不超过3450元,则该校最多可以购买多少个尤克里里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图。(要求每位同学只能选择一种自己喜欢的球类;扇形统计图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数)请你根据图中提供的信息,解答下列问题:
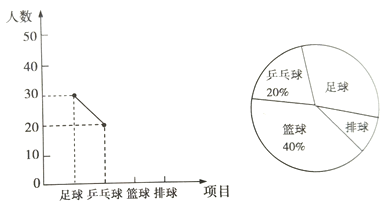
(1)在这次研究中,一共调查了多少名学生?
(2)喜欢排球的人数在扇形统计图中所对应的扇形的圆心角是多少度?
(3)补全频数分布折线统计图。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:
 =
=  .
. 
相关试题

