搜索
【题目】如图，已知AD是等腰△ABC底边BC上的中线，BC=6cm，AD=9cm，点E、F是AD的三等分点，则阴影部分的面积为______．
参考答案：
【答案】9cm2
【解析】
根据等腰三角形性质求出BD=DC=3cm，AD⊥BC，推出△CEF和△BEF关于直线AD对称，得出S△AFC=S△AFB，根据图中阴影部分的面积是
S△ABD求出即可．
解：∵BC=6cm，AD是△ABC的中线，
∴BD=DC=3cm，AD⊥BC，
∴△ABC关于直线AD对称，
∴B、C关于直线AD对称，
∴△CEF和△BEF关于直线AD对称，
∴S△AFC=S△AFB，
∵点E、F是AD的三等分点，
∴S△AFB=S△BED=
S△ABD
∴图中阴影部分的面积是S△ABD=×
×3×9=9cm2．
故答案为：9cm2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校计划购买篮球、排球共20个，购买2个篮球，3个排球，共需花费190元；购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个，所需费用总额不超过800元.请你求出满足要求的所有购买方案，并直接写出其中最省钱的购买方案
-
科目： 来源： 题型：
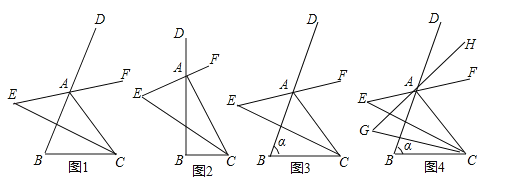
查看答案和解析>>【题目】如图，在△ABC中，分别作其内角∠ACB与外角∠DAC的角平分线，且两条角平分线所在的直线交于点E
（1）填空：①如图1，若∠B=60°，则∠E= ；
②如图2，若∠B=90°，则∠E= ；
（2）如图3，若∠B=α，求∠E的度数；
（3）如图4，仿照（2）中的方法，在（2）的条件下分别作∠EAB与∠ECB的角平分线，且两条角平分线交于点G，求∠G的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的角平分线，点E是AB边上一点，AE=AC，EF∥BC，交AC于点F．下列结论正确的是（ ）
①∠ADE=∠ADC；②△CDE是等腰三角形；③CE平分∠DEF；④AD垂直平分CE；⑤AD=CE．
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为
”表示每抛2次就有一次正面朝上C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子，朝上的点数为2的概率为
”表示随着抛掷次数的增加，“抛出朝上的点数为2”这一事件发生的频率稳定在
附近 -
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分8分）如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．
实践与操作：
根据要求尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）．
（1）作∠DAC的平分线AM；
（2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE、CF．
猜想并证明：
判断四边形AECF的形状并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的盒子里装有30个除颜色外其它均相同的球，其中红球有m个，白球有3m个，其它均为黄球．现小李从盒子里随机摸出一个球，若是红球，则小李获胜；小李把摸出的球放回盒子里摇匀，由小马随机摸出一个球，若为黄球，则小马获胜．
（1）当m=4时，求小李摸到红球的概率是多少？
（2）当m为何值时，游戏对双方是公平的？
相关试题
