Question

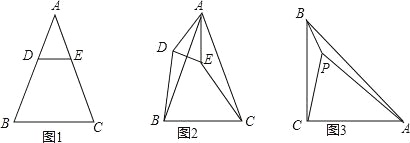
【题目】已知△ABC是等腰三角形，AB=AC．

（1）特殊情形：如图1，当DE∥BC时，有DB　　　　　　EC．（填“＞”，“＜”或“=”）

（2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．

（3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．

Answer 1

【答案】（1）=；（2）成立；（3）∠BPC =135°．

【解析】试题分析：（1）由DE∥BC，得到，结合AB=AC，得到DB=EC；

（2）由旋转得到的结论判断出△DAB≌△EAC，得到DB=CE；

（3）由旋转构造出△CPB≌△CEA，再用勾股定理计算出PE，然后用勾股定理逆定理判断出△PEA是直角三角形，在简单计算即可．

试题解析：（1）∵DE∥BC，

∴，

∵AB=AC，

∴DB=EC，

故答案为=，

（2）成立．

证明：由①易知AD=AE，

∴由旋转性质可知∠DAB=∠EAC，

又∵AD=AE，AB=AC

∴△DAB≌△EAC，

∴DB=CE，

（3）如图，

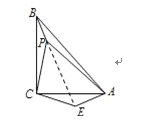
将△CPB绕点C旋转90°得△CEA，连接PE，

∴△CPB≌△CEA，

∴CE=CP=2，AE=BP=1，∠PCE=90°，

∴∠CEP=∠CPE=45°，

在Rt△PCE中，由勾股定理可得，PE=，

在△PEA中，PE2=（）2=8，AE2=12=1，PA2=32=9，

∵PE2+AE2=AP2，

∴△PEA是直角三角形

∴∠PEA=90°，

∴∠CEA=135°，

又∵△CPB≌△CEA

∴∠BPC=∠CEA=135°．