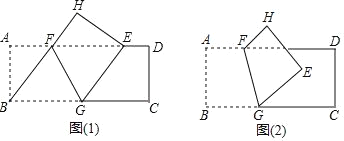
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
【答案】(1)①菱形;②4![]() ;(2)
;(2)![]()
【解析】
(1)①先证明四边形BGEF是平行四边形,再根据BG=EG,即可证得四边形BGEF是菱形;
②如图,过F作FH⊥BC于H,先证明四边形ABHF是矩形,可得FH=AB=8,再由四边形BGEF是菱形,可得BF=BG=10,在Rt△BHF中,利用勾股定理求出BH长,继而求得HG长,在Rt△FHG中,利用勾股定理即可求得FG长;
(2)设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
(1)①四边形BGEF是菱形,理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,BH∥EG,
∴四边形BGEF是平行四边形;
由折叠知,BG=EG,
∴四边形BGEF是菱形;
②如图,过F作FH⊥BC于H,

∵四边形ABCD是矩形,
∴∠A=∠ABC=∠BHF=90°,
∴四边形ABHF是矩形,
∴FH=AB=8,
由①知,四边形BGEF是菱形,
∴BF=BG=10,
在Rt△BHF中,根据勾股定理得,BH=6,
∴HG=BG﹣BH=4,
在Rt△FHG中,根据勾股定理得,FG=![]() =4
=4![]() ;
;
(2)如图,设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,
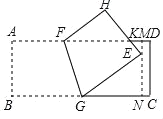
∵E到AD的距离为2,
∴EM=2,EN=8﹣2=6,
在Rt△ENG中,GN=![]() =8,
=8,
∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,
∠GEN+∠NGE=180°﹣90°=90°,
∴∠KEM=∠NGE,
又∵∠ENG=∠KME=90°,
∴△GEN∽△EKM,
∴![]() ,
,
即![]() ,
,
解得EK=![]() ,KM=
,KM=![]() ,
,
∴KH=EH﹣EK=8﹣![]() =
=![]() ,
,
∵∠FKH=∠EKM,∠H=∠EMK=90°,
∴△FKH∽△EKM,
∴![]() ,
,
即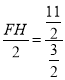 ,
,
解得FH=![]() ,
,
∴AF=FH=![]() .
.

