【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
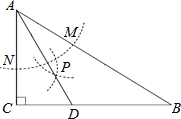
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】A.
【解析】
试题解析:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,

∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
∵∠2=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∴BD=2CD.
故④正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(﹣7m+A)(4n+B)=16n2﹣49m2,则A=________,B=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】样本2,6,6,8,10,6,10,10的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线
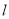 ∥PQ,点D在点C的左边且CD=3.
∥PQ,点D在点C的左边且CD=3.(1) 直接写出△BCD的面积.
(2) 如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,则∠CEF与∠CFE有何数量关系?请说明理由.
(3) 如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中
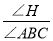 的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

-
科目: 来源: 题型:
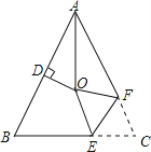
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
相关试题

