Question

【题目】如图，已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．

（1）求抛物线的解析式及它的对称轴；

（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；

（3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=-x2+x+4，x=3；（2）C（0，4）；y=x+4．（3）Q1（3，0），Q2（3，4+），Q3（3，4-）．

【解析】

试题分析：（1）利用待定系数法求出抛物线解析式，利用配方法或利用公式x=求出对称轴方程；

（2）在抛物线解析式中，令x=0，可求出点C坐标；令y=0，可求出点B坐标．再利用待定系数法求出直线BD的解析式；

（3）本问为存在型问题．若△ACQ为等腰三角形，则有三种可能的情形，需要分类讨论，逐一计算，避免漏解．

（1）∵抛物线y=-x2+bx+4的图象经过点A（-2，0），

∴-×（-2）2+b×（-2）+4=0，

解得：b=，

∴抛物线解析式为 y=-x2+x+4，

又∵y=-x2+x+4=-（x-3）2+，

∴对称轴方程为：x=3．

（2）在y=-x2+x+4中，令x=0，得y=4，

∴C（0，4）；

令y=0，即-x2+x+4=0，整理得x2-6x-16=0，解得：x=8或x=-2，

∴A（-2，0），B（8，0）．

设直线BC的解析式为y=kx+b，

把B（8，0），C（0，4）的坐标分别代入解析式，得：

，

解得，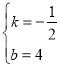

∴直线BC的解析式为：y=x+4．

∵抛物线的对称轴方程为：x=3，

可设点Q（3，t），则可求得：

AC=，

AQ=，

CQ=．

i）当AQ=CQ时，有=，

25+t2=t2-8t+16+9，

解得t=0，

∴Q1（3，0）；

ii）当AC=AQ时，有

t2=-5，此方程无实数根，

∴此时△ACQ不能构成等腰三角形；

iii）当AC=CQ时，有，

整理得：t2-8t+5=0，

解得：t=4±，

∴点Q坐标为：Q2（3，4+），Q3（3，4-）．

综上所述，存在点Q，使△ACQ为等腰三角形，点Q的坐标为：Q1（3，0），Q2（3，4+），Q3（3，4-）．