【题目】已知如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形的面积. 
参考答案:
【答案】解:连接AC,如图所示: 
∵∠B=90°,∴△ABC为直角三角形,
又AB=4,BC=3,
∴根据勾股定理得:AC= ![]() =5,
=5,
又AD=13,CD=12,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2 ,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD= ![]() ABBC+
ABBC+ ![]() ACCD=
ACCD= ![]() ×3×4+
×3×4+ ![]() ×12×5=36
×12×5=36
【解析】连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
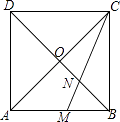
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
A.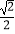
B.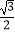
C.1
D.
-
科目: 来源: 题型:
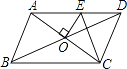
查看答案和解析>>【题目】如图,ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=13cm,AC=15cm,高AD=12cm.则△ABC的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=
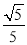 ,求BD的长.
,求BD的长. 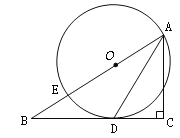
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
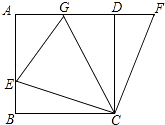
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
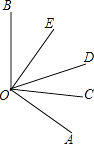
(1)若∠AOB=120°,则∠COE是多少度?
(2)若∠EOC=65°,∠DOC=25°,则∠BOE是多少度?
相关试题

