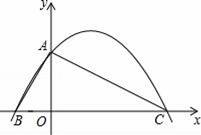
已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点G是对称轴上一点,求当△GAB周长最小时,点G的坐标;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,并选择其中一个的加以说明;若不存在,说明理由;
(4)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A、B、M、N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由.

【考点】二次函数综合题.
【分析】(1)由线段长度求出三个点的坐标,再用待定系数法求解即可;
(2)找到点B关于抛物线对称轴的对称点A,取AB与抛物线对称轴的交点即可;
(3)分别过点P,A作AP的垂线,取点Q,根据等腰直角三角形构建全等三角形即可求解;
(4)根据以AB为边和以AB为对角线进行讨论,结合菱形的性质进行求解即可.
【解答】解:(1)由题意可求,A(0,2),B(﹣1,0),点C的坐标为(4,0).
设过A、B、C三点的抛物线的解析式为y=a(x﹣4)(x+1),
把点A(0,2)代入,解得:a=﹣
 ,
,
所以抛物线的解析式为:y=﹣
 (x﹣4)(x+1)=
(x﹣4)(x+1)=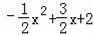
 ,
,
(2)如图1
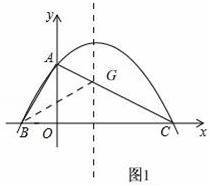

物线y=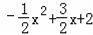
 的对称轴为:x=
的对称轴为:x=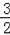
 ,
,
由点C是点B关于直线:x=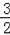
 的对称点,所以直线AC和直线x=
的对称点,所以直线AC和直线x=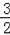
 的交点即为△GAB周长最小时的点G,
的交点即为△GAB周长最小时的点G,
设直线AC的解析式为:y=mx+n,把A(0,2),点C(4,0)代入得:.
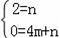
 ,
,
解得: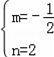
 ,
,
所以:y=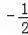
 x+2,
x+2,
当x=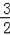
 时,y=
时,y=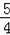
 ,
,
所以此时点G(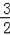
 ,
,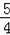
 );
);
(3)如图2
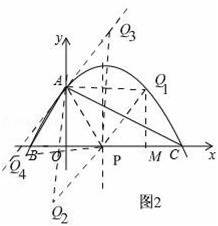

使△PAQ是以PA为腰的等腰直角三角形的所有符合条件的点Q的坐标:Q1(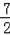
 ,
,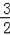
 ),Q2(
),Q2(
 ,﹣
,﹣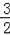
 ),Q3(2,
),Q3(2,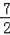
 ),Q4(﹣2,
),Q4(﹣2,
 ),
),
证明Q1:过点Q1作Q1M⊥x轴,垂足为M,
由题意:∠APQ1=90°,AP=PQ1,
∴∠APO+∠MPQ1=90°,
∵∠APO+∠PAO=90°,
∴∠PAO=∠MPQ1,
在△AOP和△MPQ1中,
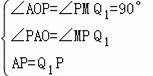
 ,
,
∴△AOP≌△MPQ1,
∴PM=AO=2,Q1M=OP=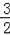
 ,
,
∴OM=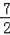
 ,
,
此时点Q的坐标为:(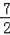
 ,
,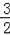
 );
);
(4)存在
点N的坐标为:(0,﹣2),(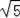
 ,2),(﹣
,2),(﹣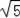
 ,2),(
,2),(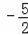
 ,2).
,2).
【点评】此题主要考查二次函数的综合问题,会运用待定系数法求函数解析式;结合对称点解决线段和最小问题;熟悉等腰直角三角形的性质,并应用于点的存在的研究;熟悉菱形的性质,并运用于菱形顶点的存在性研究是解决此题的关键.

