10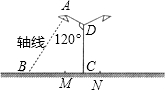．要在宽为36m的公路的绿化带MN（宽为4m）的中央安装路灯，路灯的灯臂AD的长为3m，且与灯柱CD成120°（如图所示），路灯采用圆锥形灯罩，灯罩的轴线AB与灯臂垂直．当灯罩的轴线通过公路路面一侧的中间时（除去绿化带的路面部分），照明效果最理想，问：应设计多高的灯柱，才能取得最理想的照明效果？（精确到0.01m，参考数据$\sqrt{3}$≈1.732）

分析 延长BA，CD交于点P，解直角三角形得到AP=PD•cos30°和BC的长，通过△PAD∽△PCB，得出$\frac{AP}{PC}$=$\frac{AD}{BC}$，代入数据即可得到结论．

解答 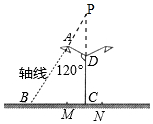解：如图，延长BA，CD交于点P，
∵∠PAD=∠PCB=90°，∠ADC=120°，
∴∠P=30°，
∵AD=3，
∴PD=6，AP=PD•cos30°=3$\sqrt{3}$，
BC=（18-2）÷2+2=10．
∵∠P=∠P，∠PAD=∠PCB=90°，
∴△PAD∽△PCB，
∴$\frac{AP}{PC}$=$\frac{AD}{BC}$，
∴PC=$\frac{AP•BC}{AD}$=10$\sqrt{3}$m，
∴CD=PC-PD=10$\sqrt{3}$-6≈11.32m．
则应设计11.32m高的灯柱，才能取得最理想的照明效果．

点评 本题考查了相似三角形的性质，直角三角形的性质，锐角三角函数的概念，正确的作出辅助线构造相似三角形是解题的关键．

关闭