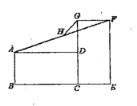
【题目】矩形![]() 与矩形
与矩形![]() 如图放置,点
如图放置,点![]() 共线,点
共线,点![]() 共线,连接
共线,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的长为
的长为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
延长GH交AD于点P,先证△APH≌△FGH得AP=GF=1,GH=PH=![]() PG,再利用勾股定理求得PG=2
PG,再利用勾股定理求得PG=2![]() ,从而得出答案.
,从而得出答案.
解:如图,延长GH交AD于点P,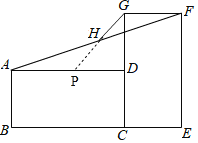
∵四边形ABCD和四边形CEFG都是矩形,
∴∠ADC=∠ADG=∠CGF=90°,AD=BC=3、GF=CE=1,
∴AD∥GF,
∴∠GFH=∠PAH,
又∵H是AF的中点,
∴AH=FH,
在△APH和△FGH中,
∵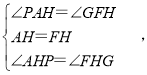
∴△APH≌△FGH(ASA),
∴AP=GF=1,GH=PH=![]() PG,
PG,
∴PD=AD-AP=3-1=2,
∵CG=EF=3、CD=1,
∴DG=2,△DGP是等腰直角三角形,
则GH=![]() PG=
PG= ![]() ×
×![]()
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数;
(2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2 ;
(3)在图②中,若AG=12, BM=
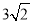 ,直接写出MN的值.
,直接写出MN的值.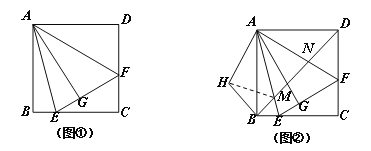
-
科目: 来源: 题型:
查看答案和解析>>【题目】小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中,恰好四个顶点都在横格线上,已知a=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
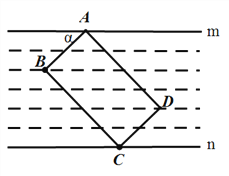
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
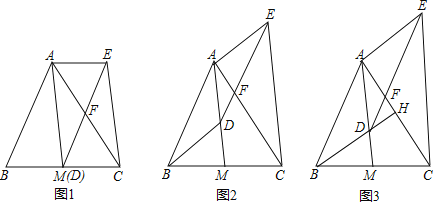
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=
 , DM=4时,求DH的长.
, DM=4时,求DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如表:

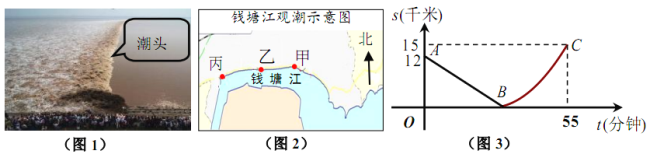
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离
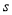 (千米)与时间
(千米)与时间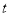 (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点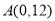 ,点
,点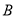 坐标为
坐标为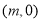 ,曲线
,曲线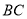 可用二次函数
可用二次函数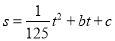 (
(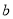 ,
,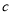 是常数)刻画.
是常数)刻画.(1)求
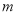 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
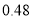 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
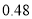 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度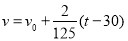 ,
,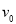 是加速前的速度).
是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, ,
, 交
交 于
于 ,
, 平分
平分 ,
, ,下面结论:①
,下面结论:① ;②
;② 是等边三角形;③
是等边三角形;③ ;④
;④ ,其中正确的有
,其中正确的有
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
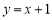 与
与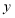 轴交于点
轴交于点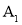 ,依次作正方形
,依次作正方形 、正方形
、正方形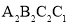 、……正方形
、……正方形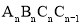 ,使得点
,使得点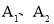 、…,
、…,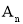 在直线
在直线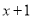 上,点
上,点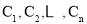 在
在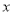 轴上,则点
轴上,则点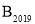 的坐标是________
的坐标是________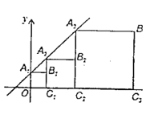
相关试题

