【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点于
轴交点于![]() ,且
,且![]() ,
,![]() °,以
°,以![]() 为边长作等边三角形
为边长作等边三角形![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边三角行
为边长作等边三角行![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]()
![]() 为边长坐等三角形
为边长坐等三角形![]() ,…,则点
,…,则点![]() 的横坐标是___________.
的横坐标是___________.
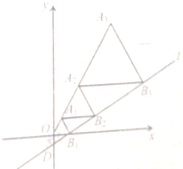
参考答案:
【答案】![]()
【解析】过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为![]() ,,A2的横坐标为
,,A2的横坐标为![]() , A3的横坐标为
, A3的横坐标为![]() ,进而得到An的横坐标为
,进而得到An的横坐标为![]() ,据此可得点A10的横坐标.
,据此可得点A10的横坐标.
解:如图所示,过A1作A1A⊥OB1于A,则OA=![]() OB1=
OB1=![]() ,
,

即A1的横坐标为![]() =
=![]() ,
,
∵![]() °,
°,
∴∠OB1D=30°,
∵A1B2//x轴,
∴∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=![]() A1B2=1,
A1B2=1,
即A2的横坐标为![]() +1=
+1=![]() ,
,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=![]() A2B3=2,
A2B3=2,
即A3的横坐标为![]() +1+2=
+1+2=![]() ,
,
同理可得,A4的横坐标为![]() +1+2+4=
+1+2+4=![]() ,
,
由此可得,An的横坐标为![]() ,
,
∴点A10的横坐标是![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为4和6,则第三边可能是( )
A. 2 B. 7 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三个内角的度数分别为40°,60°,80°,则这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)
分)(
 )【问题】如图
)【问题】如图 ,点
,点 为线段
为线段 外一动点,且
外一动点,且 ,
,  .当点
.当点 位于__________时线段
位于__________时线段 的长取得最大值,且最大值为__________(用含
的长取得最大值,且最大值为__________(用含 、
、 的式子表示).
的式子表示).(
 )【应用】点
)【应用】点 为线段
为线段 除外一动点,且
除外一动点,且 ,
,  .如图
.如图 所示,分别以
所示,分别以 、
、 为边,
为边,作等边三角形
 和等边三角形
和等边三角形 ,连接
,连接 、
、 .
.①请找出图中与
 相等的线段,并说明理由.
相等的线段,并说明理由.②直接写出线段
 长的最大值.
长的最大值.(
 )【拓展】如图
)【拓展】如图 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,点
,点 为线段
为线段 外一动点,且
外一动点,且 ,
,  ,
,  .请直接写出线段
.请直接写出线段 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.



-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)
分)如图,在
 中,
中,  ,
,  ,
,  ,将
,将 绕点
绕点 按逆时针方向旋转至
按逆时针方向旋转至 ,
,  点的坐标为
点的坐标为 .
.
(
 )求
)求 点的坐标.
点的坐标.(
 )求过
)求过 ,
,  ,
,  三点的抛物线
三点的抛物线 的解析式.
的解析式.(
 )在(
)在( )中的抛物线上是否存在点
)中的抛物线上是否存在点 ,使以
,使以 ,
,  ,
,  为顶点的三角形是等腰直角三角形?若
为顶点的三角形是等腰直角三角形?若存在,求出所有点
 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】温度从-2℃上升3℃后是( )
A. 1℃B. -1℃C. 3℃D. 5℃
相关试题

