【题目】如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 ( )

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
参考答案:
【答案】B
【解析】
作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,再根据AD是∠BAC的平分线可知M′H=M′N′,再由锐角三角函数的定义即可得出结论.
如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,
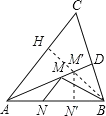
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵![]()
∴![]()
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH![]()
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.

(1)若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接运动会,某校八年级学生开展了“短跑比赛”。甲、乙两人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度
 与
与 。
。甲前一半的路程使用速度
 ,另一半的路程使用速度
,另一半的路程使用速度 ;乙前一半的时间用速度
;乙前一半的时间用速度 ,另一半的时间用速度
,另一半的时间用速度 。
。(1)甲、乙二人从A地到达B地的平均速度分别为
 ;则
;则 ___________,
___________, ____________
____________(2)通过计算说明甲、乙谁先到达B地?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
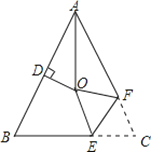
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA=3,PB=4,PC=5,连接PQ,试判断△PQC的形状,并说明理由。

相关试题

