【题目】安岳是有名的“柠檬之乡”,某超市用3000元进了一批柠檬销售良好;又用7700元购来一批柠檬,但这次的进价比第一批高了10%,购进数量是第一批的2倍多500斤.
(1)第一批柠檬的进价是每斤多少元?
(2)为获得更高利润,超市决定将第二批柠檬分成大果子和小果子分别包装出售,大果子的售价是第一批柠檬进价的2倍,小果子的售价是第一批柠檬进价的1.2倍.问大果子至少要多少斤才能使第二批柠檬的利润不低于3080元?
参考答案:
【答案】(1)2元;(2)至少要1487.5斤.
【解析】
(1)设第一批柠檬的进价是每斤x元,根据第二次购进数量是第一批的2倍多500斤即可得出分式方程求出答案;
(2)首先求出第二批柠檬的数量,第二批柠檬的进价,大果子每斤利润和小果子每斤利润,进而根据利润不低于3080元得出不等式解答即可.
解:(1)设第一批柠檬的进价是每斤x元,
据题意得:![]() ,
,
解得:x=2
经检验,x=2是原方程的解且符合题意
答:第一批柠檬的进价是2元每斤;
(2)第二批柠檬的数量为:7700÷2(1+10%)=3500(斤),
第二批柠檬的进价为:2(1+10%)=2.2元,
大果子每斤利润为2×2-2.2=1.8元,小果子每斤利润为2×1.2-2.2=0.2元,
设大果子的数量为y斤才能使第二批柠檬的利润不低于3080元,
根据题意得:1.8y+(3500y)×0.2≥3080,
解得:y≥1487.5,
答:大果子至少要1487.5斤才能使第二批柠檬的利润不低于3080元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点M、N是BC、CD边上的点,连接AM、BN,若BM=CN

(1)求证:AM⊥BN
(2)将线段AM绕M顺时针旋转90°得到线段ME,连接NE,试说明:四边形BMEN是平行四边形;
(3)将△ABM绕A逆时针旋转90°得到△ADF,连接EF,当
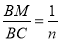
 时,请求出
时,请求出 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程,并解答后面的问题:
如图,在平面直角坐标系中,
 ,
,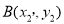 ,C为线段AB的中点,求C的坐标.解:分别过A,C作x轴的平行线,过B,C作y轴的平行线,两组平行线的交点如图1.
,C为线段AB的中点,求C的坐标.解:分别过A,C作x轴的平行线,过B,C作y轴的平行线,两组平行线的交点如图1.设C的坐标为
 ,则D、E、F的坐标为
,则D、E、F的坐标为 ,
,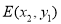 ,
,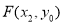
由图可知:
 ,
,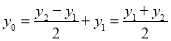
∴C的坐标为

问题:
(1)已知A(-1,4),B(3,-2),则线段AB的中点坐标为______
(2)平行四边形ABCD中,点A、B、C的坐标分别为(1,-4),(0,2),(5,6),求D的坐标.
(3)如图2,B(6,4)在函数
 的图象上,A的坐标为(5,2),C在x轴上,D在函数
的图象上,A的坐标为(5,2),C在x轴上,D在函数 的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)分别求出两种优惠方案中y与x之间的关系式;
(2)购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
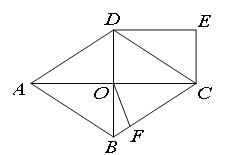
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,双曲线
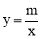 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.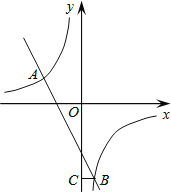
(1)求双曲线和直线的解析式;
(2)直接写出不等式
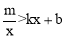 的解集.
的解集.
相关试题

