【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.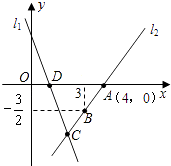
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
参考答案:
【答案】
(1)解:∵点A(4,0)、B(3,﹣ ![]() )在直线l2:y2=kx+b上,
)在直线l2:y2=kx+b上,
∴ 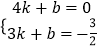 ,
,
解得: 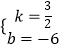 .
.
∴直线l2的解析式为y2= ![]() x﹣6;
x﹣6;
由 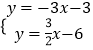 ,
,
解得 ![]() .
.
∴点C的坐标为(2,﹣3)
(2)解:∵点D是直线l1:y=﹣3x+3与x轴的交点,
∴y=0时,0=﹣3x+3,解得x=1,
∴D(1,0),
∵A(4,0),
∴AD=4﹣1=3,
∴△ADC的面积= ![]() ×3×3=
×3×3= ![]()
(3)解:由图象可知,当x<2时,y1>y2
(4)解:符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3),
①以AC为对角线时,
∵四边形ADCE是平行四边形,
∴CE∥DA,CE=DA=3,
∴将点C(2,﹣3)向右平移3个单位得到点E,即E1(5,﹣3);
②以AD为对角线时,
∵四边形ACDE是平行四边形,
∴CE与AD互相平分,即CE与AD的中点重合,则E2(3,3);
③以CD为对角线时,
∵四边形ADEC是平行四边形,
∴CE∥AD,CE=AD=3,
∴将点C(2,﹣3)向左平移3个单位得到点E,即E3(﹣1,﹣3);
综上所述,符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3)
【解析】(1)由题意可知直线l2经过点A,B,利用待定系数法建立方程组求解即可;由直线l1的函数表达式和直线l2的函数解析式联立方程,求解即可得出点C的坐标。
(2)先求出点D的坐标,再求出AD的长,然后就可以求出△ADC的面积。
(3)由点C的坐标为(2,﹣3),因此观察直线x=2左右两侧的图像,即可得出y1>y2时,x的取值范围。
(4)此小题分三种情况:①以AC为对角线时;②以AD为对角线时;③以CD为对角线时;根据平行四边形的性质就可以求出满足条件的点E的坐标。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
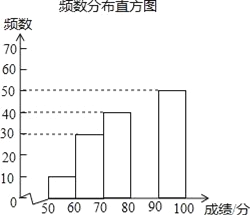
-
科目: 来源: 题型:
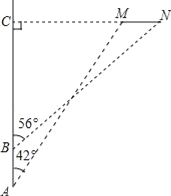
查看答案和解析>>【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l外一点P与直线l上两点的连线段长分别为3cm,5cm,则点P到直线l的距离是( )
A. 不超过3cmB. 3cmC. 5cmD. 不少于5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算“※”:x※y=xy+x2﹣y2 , 化简(2a+3b)※(2a﹣3b),并求出当a=2,b=1时的值.
相关试题

