搜索
【题目】平行四边形的周长为24，相邻两边的差为2，则平行四边形的各边长为（ ）．
A.4，4，8，8
B.5，5，7，7
C.5.5，5.5，6.5，6.5
D.3，3，9，9
参考答案：
【答案】B
【解析】
平行四边形的对边相等，所以两邻边的和为周长的一半．周长为24，则两邻边的和为12．又因为相邻的两边相差2，则可计算出较长的一边为7，较短的一边长为5．所以选B
本题考查平行四边形的性质．掌握平行四边形对边相等，且两邻边之和等于周长的一半，就能解答本题
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
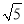，求AC的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一根弹簧原长10厘米，挂重物后（不超过50克），它的长度会改变，请根据下面表格中的一些数据回答下列问题：
质量（克）
1
2
3
4
……n
伸长量（厘米）
0．5
1
1．5
2
……
总长度（厘米）
10．5
11
11．5
12
……
（1）要想使弹簧伸长5厘米，应挂重物多少克？
（2）当所挂重物为x克时，用代数式表示此时弹簧的总长度．
（3）当x=30克时，求此时弹簧的总长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平行四边形的两邻角的角平分线相交所成的角为（ ）．
A.锐角
B.直角
C.钝角
D.不能确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】(2016浙江省舟山市第23题)我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”
（1）概念理解：
请你根据上述定义举一个等邻角四边形的例子；
（2）问题探究；
如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；
（3）应用拓展；
如图2，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt△ABD绕着点A顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt△AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．
-
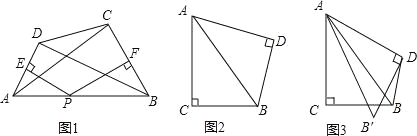
科目： 来源： 题型：
查看答案和解析>>【题目】根据某手机收费标准，从甲地向乙地打长途电话，前3分钟收费1．8元，3分钟后每分钟加收费0．8元．
（1）若通话时间为x分钟（x≥3），则应收费多少元？
（2）若小王按此标准打一个电话花了8．2元，则这个电话小王打了几分钟？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种商品，由于进价降低了5%，出售价不变，使得利润由m%提高到（m+6）%，则m的值为（ ）
A.10
B.12
C.14
D.17
相关试题
