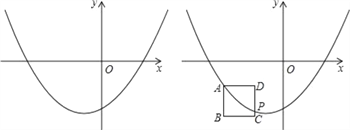
【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).
发现:(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为 ;
(2)抛物线的对称轴为直线x= (用含b的代数式表示),位于y轴的 侧.
思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y=![]() (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式.
参考答案:
【答案】发现:(1) (0,﹣3);(2)b,左;思考:10<k<36;探究:b=![]() .
.
【解析】试题分析:解:(1)抛物线与y轴的交点为定点;当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)利用抛物线的对称轴方程得到抛物线的对称轴为直线x=b,然后利用b的范围确定抛物线的对称轴在y轴的左侧;
思考:把P点坐标代入y=x2﹣2bx﹣3得b=﹣1,则抛物线解析式为y=x2+2x﹣3,再分别计算出a=2和a=3所对应的二次函数值,从而确定反比例函数与抛物线的交点的位置,然后利用反比例函数图象上点的坐标特征确定k的范围;
探究:设A(m,m2+2m﹣3),利用正方形的性质得D(m+1,m2+2m﹣3),则P点的坐标为(m+1,﹣3),然后把P(m+1,﹣3)代入y=x2﹣2bx﹣3可得到b与m的关系式.
试题解析:解:(1)当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)抛物线的对称轴为直线x=﹣![]() =b,
=b,
因为b<0,
所以抛物线的对称轴在y轴的左侧;
故答案为(0,﹣3),b,左;
思考:把P(﹣2,﹣1)代入y=x2﹣2bx﹣3得4+4b﹣3=﹣1,解得b=﹣1,
抛物线解析式为y=x2+2x﹣3,
当a=2时,y=x2+2x﹣3=4+4﹣3=5,
当a=3时,y=x2+2x﹣3=9+6﹣3=12,
所以二次函数图象与反比例函数的交点在抛物线上的点(2,5),(3,12)之间,
所以2×5<k<3×12,
即10<k<36;
探究:设A(m,m2+2m﹣3),
∵正方形ABCD的边长为1,AB⊥x轴,
∴D(m+1,m2+2m﹣3),
∴P点的坐标为(m+1,﹣3),
把P(m+1,﹣3)代入y=x2﹣2bx﹣3得(m+1)2﹣2b(m+1)﹣3=﹣3,
而m+1≠0,
∴m+1﹣2b=0,
∴b=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】收集数据的方法是( )
A.查资料
B.做实验
C.做调查
D.以上三者都是 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三条边的长分别是2,x,6,则整数x的值有__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要调查某校七年级学生周日的睡眠时间,选取调查对象最合适的是( )
A.选取七年级一个班级的学生
B.选取50名七年级男生
C.选取50名七年级女生
D.随机选取50名七年级学生 -
科目: 来源: 题型:
查看答案和解析>>【题目】利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查,共发放问卷300份(问卷由单选和多选题组成),对收回的265份问卷进行了整理,部分数据如下:
(1)最近一次购买各品牌纯牛奶用户比例如图:

(2)用户对各品牌纯牛奶满意情况汇总如下表:
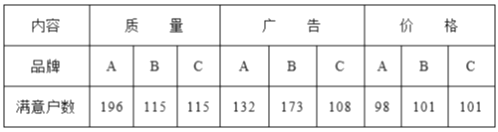
结合上述信息回答下列问题:
①A品牌牛奶的主要竞争优势是什么?请简要说明理由.
②广告对用户选择品牌有影响吗?请简要说明理由.
③你对厂家C有何建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列统计活动中不宜用问卷调查的方式收集数据是( )
A.七年级同学家中电脑的数量
B.星期六早晨同学们起床的时间
C.各种手机在使用时所产生的辐射
D.学校足球队员的年龄和身高 -
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
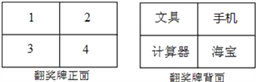
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
相关试题

