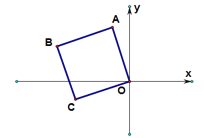
【题目】(10分)如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣4,﹣2),
(1)求点A的坐标.
(2)线段BO的长度.
参考答案:
【答案】(1)A(-2,4);(2)2![]()
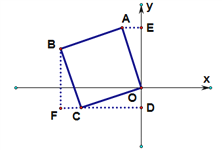
【解析】试题分析:(1)过点A作AE⊥y轴,垂足为E,过点C作CD⊥y轴,垂足为D,易证△AEO△ODC,即可求得A点的坐标;(2)过点B作BF⊥CD交DC的延长线于点F,易证△BFC△ODC,即可求得点B的坐标,由勾股定理求得正方形的边长,即可求得正方形的对角线OB的长.
试题解析:
(1)过点A作AE⊥y轴,垂足为E,过点C作CD⊥y轴,垂足为D,
易证△AEO![]() △ODC,得A(-2,4);
△ODC,得A(-2,4);
(2)同理可证△BFC![]() △ODC,得B(-6,2),得BO=
△ODC,得B(-6,2),得BO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10 台和
液晶显示器8台,共需要资金7000 元;若购进电脑机箱2台和液晶显示器5台,共需要资金
4120元.
(1)每合电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元. 根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元. 该经销商希望销售完这两种商品,所获利润不少于4100元. 试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
-
科目: 来源: 题型:
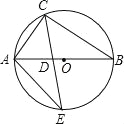
查看答案和解析>>【题目】(2016山东省泰安市第17题)如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1:
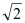 B.1:
B.1: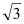 C.1:2 D.2:3
C.1:2 D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面的性质中,平行四边形不一定具有的是( ).
A.对角互补
B.邻角互补
C.对角相等
D.对边相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知-xm+3y与2x4yn+3是同类项,求(m+n)2018的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果收入50元,记作+50元,那么支出30元记作( )
A.+30元
B.﹣30元
C.+80元
D.﹣80元 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省泰安市第22题)如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .

相关试题

