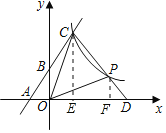
【题目】如图，一次函数y＝k1x+3的图象与坐标轴相交于点A（﹣2，0）和点B，与反比例函数y＝（x＞0）相交于点C（2，m）．

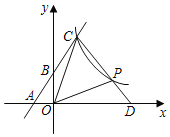
（1）填空：k1＝　 　，k2＝　 　；

（2）若点P是反比例函数图象上的一点，连接CP并延长，交x轴正半轴于点D，若PD：CP＝1：2时，求△COP的面积．

【答案】（1），12；（2）S△COP＝16．

【解析】

（1）先根据点A求出k1，再根据一次函数解析式求出m值，利用待定系数法求反比例函数的解析式；
（2）先根据三角形相似求得P点的坐标，然后利用三角形的面积差求解．S△COP=S△COD-S△POD．

（1）∵一次函数y＝k1x+3的图象与坐标轴相交于点A（﹣2，0），

∴﹣2k1+3＝0，

解得k1＝，

∴一次函数为：y1＝x+3，

∵一次函数y1＝x+3的图象经过点C（2，m）．

∴m＝×2+3＝6，

∴C点坐标为（2，6），

∵反比例函数y＝（x＞0）经过点C，

∴k2＝2×6＝12，

故答案为，12．

（2）作CE⊥OD于E，PF⊥OD于F，

∴CE∥PF，

∴△PFD∽△CED，

∴＝，

∵PD：CP＝1：2，C点坐标为（2，6），

∴PD：CD＝1：3，CE＝6，

∴＝，

∴PF＝2，

∴P点的纵坐标为2，

把y＝2代入y2＝求得x＝6，

∴P（6，2），

设直线CD的解析式为y＝ax+b，

把C（2，6），P（6，2）代入得，

解得，

∴直线CD的解析式为y＝﹣x+8，

令y＝0，则x＝8，

∴D（8，0），

∴OD＝14，

∴S△COP＝S△COD﹣S△POD＝×8×6﹣＝16．

关闭