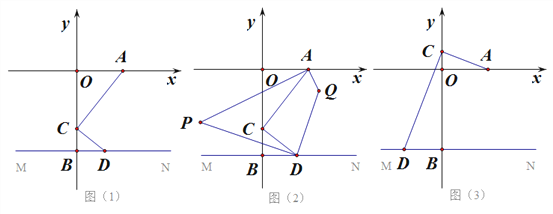
【题目】如图,在平面直角坐标系中,点A在X轴正半轴上,B在Y轴的负半轴,过点B画MN∥x轴;C是Y轴上一点,连接AC,作CD⊥CA.
(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.
(2)如图(2),在题(1)的条件下,∠CAO的角平分线与∠CDB的角平分线相交于点P,求∠APD的度数.
(3)如图(2),在题(1)、(2)的条件下,∠CAX的角平分线与∠CDN的角平分线相交于点Q,请直接写出∠APD与∠AQD数量关系.
(4)如图(3),点C在Y轴的正半轴上运动时,∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P,∠APD的大小是否变化?若不变,直接写出其值;若变化,说明理由.
参考答案:
【答案】(1)∠CAO+∠CDB=90;
(2)∠APD=45;
(3)∠APD+∠AQD=180;
(4)∠APD的大小不变,为45.
【解析】试题分析:(1)根据平行线的性质可直接写出结果;
(2)根据(1)的结论,由角平分线的性质可直接求解;
(3)根据(1)(2)的结论,由角平分线的性质可直写出结果;
(4)同上面的解题方法,直接判断即可.
试题解析:(1)∠CA0+∠CDB=90
(2)∠APD=45
(3)∠APD+∠AQD=180
(4)∠APD的大小不变,为45
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+3|+(b-1)2=0,则3a+b=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣
 x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以
x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以 个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.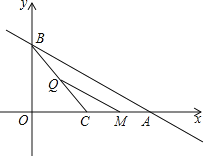
(1)∠BCO= °;
(2)求y关于t的函数关系式及自变量t的取值范围;
(3)是否存在时间t,使得以PC为直径的⊙D与直线QM相切?若存在,求t的值;不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点E在正方形ABCD的边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在图2的AB边上是否存在一点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.我校上月举办了“读书节”活动。为了表彰优秀,主办单位王老师负责购买奖品.他发现:若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品.设钢笔单价为x元/支,笔记本单价为y元/本.
(1)请用x的代数式表示y.
(2)若用这钱全部购买笔记本,总共可以买几本?
(3)若王老师用这钱恰好买30份同样的奖品,可以选择a支钢笔和b本笔记本作为一份奖品(两种奖品都要有),请求出所有可能的a、b值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.

(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地去年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值( )
A. 精确到亿位 B. 精确到百分位
C. 精确到千万位 D. 精确到百万位
相关试题

