搜索
【题目】有四个命题：①相等的角是对顶角②两条直线被第三条直线所截，同位角相等③同一种四边形一定能进行平面镶嵌；④垂直于同一条直线的两条直线互相平行．其中真命题的个数为（ ）
A. 2B. 1C. 3D. 4
参考答案：
【答案】B
【解析】
根据对顶角的性质，平行线的性质，镶嵌的知识，逐一判断．
①对顶角有位置及大小关系，相等的角不一定是对顶角，假命题；
②只有当两条平行直线被第三条直线所截，同位角相等，假命题；
③同一种四边形内角和为360°，且对应边相等，一定能进行平面镶嵌，真命题；
④在同一平面内，垂直于同一条直线的两条直线平行，假命题．
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x轴于点A2；
将C2绕点A2旋转180°得C3，交x轴于点A3；
…
如此进行下去，直至得C13．若P（37，m）在第13段抛物线C13上，则m=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：
(1)－9x3y2－6x2y2＋3xy； (2)4x2－25y2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：
①a2(x﹣y)+4b2(y﹣x)
②2a3-8a2+8a
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知m+n=2，mn=-2，则（1-m）（1-n）=。
-
科目： 来源： 题型：
查看答案和解析>>【题目】（12分）如图，在平面直角坐标系中，二次函数
的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点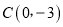
，点P是直线BC下方抛物线上的一个动点．（1）求二次函数解析式；
（2）连接PO，PC，并将△POC沿y轴对折，得到四边形
.是否存在点P，使四边形
为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：5x2﹣20= ．
相关试题
