【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)每月产销量y(个)与销售单价x(元)之间的函数关系式为; 从上表可知,每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价最低为多少元?
参考答案:
【答案】
(1)y=﹣2x+860
(2)解:当Q=30时,y=320,由(1)可知y=﹣2x+860,所以x=270,即销售单价为270元,
由于 ![]() =
= ![]() ,
,
∴成本占销售价的 ![]() .
.
(3)解:若y≤400,则Q≥ ![]() ,即Q≥24,固定成本至少是24元,
,即Q≥24,固定成本至少是24元,
400≥﹣2x+860,解得x≥230,即销售单价最低为230元.
【解析】解;(1)由于销售单价每降低1元,每月可多售出2个,所以月产销量y(个)与销售单价x (元)之间存在一次函数关系,不妨设y=kx+b,则(280,300),(279,302)满足函数关系式,得 ![]() , 解得
, 解得 ![]() ,
,
产销量y(个)与销售单价x (元)之间的函数关系式为y=﹣2x+860.
观察函数表可知两个变量的乘积为定值,所以固定成本Q(元)与月产销量y(个)之间存在反比例函数关系,不妨设Q= ![]() ,将Q=60,y=160代入得到m=9600,
,将Q=60,y=160代入得到m=9600,
此时Q= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
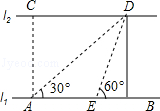
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱,标有5,6,7的三个球放入乙箱中.

(1)小宇从甲箱中随机摸出一个球,则“摸出标有数字是5的球”的概率是;
(2)小宇从甲箱中,小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字小于1,则称小宇“屡胜一筹”,请你用列表法(或画树状图),求小宇“屡胜一筹”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1B1C1 , AB与A1C1相交于点D,A1C1、BC1与AC分别交于点E、F.

(1)求证:△BCF≌△BA1D;
(2)当∠C=40°时,请你证明四边形A1BCE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上,Rt△ABC与直径为CE的半圆O,如图1摆放,∠B=90°,BC=m,AC=2CE=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转,且∠ECD=∠ACB,旋转角记为α(0°≤α≤180°).

(1)①当α=0°时,连接DE,则∠CDE=°,CD=;②当α=180°时, = .
= .
(2)试判断:旋转过程中 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)若m=4,n=5,当α=∠ACB时,线段BD= .
(4)若m=4 ,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .
,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y=
 (3≤x≤12)的一部分,记作G1 , 且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2 .
(3≤x≤12)的一部分,记作G1 , 且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2 . 
(1)求双曲线的解析式;
(2)设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为;
(3)点(6,n)为G1与G2的交点坐标,求a的值.
(4)解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN< ,直接写出a的取值范围.
,直接写出a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )

A.45°
B.50°
C.60°
D.75°
相关试题

