【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素c含量及购买这两种原料的价格如下表:

现要配制这种营养食品20 千克,要求每千克至少含有480 单位的维生素c,设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y 元,求 y与x的函数关系式,并说明购买甲种原料多少千克时,总费用最少。
参考答案:
【答案】(1)至少需要购买甲种原料8千克;
(2)y=9x+5(20-x)=4x+100(8≤x≤20),当x=8时,y最小,最小费用为132元。
【解析】试题分析:(1)根据题意分别求出甲、乙两种原料中维生素C的含量,再根据每千克至少含有480单位的维生素C,列出不等式即可;(2)根据表中所给的数据列出式子,再根据k的值,即可得出购买甲种原料多少千克时,总费用最少.
试题解析:(1)设购买甲种原料x千克.需购买乙种原料(20-x)千克。
则600x+400(20-x)≥480×20,
得: x≥8,
∴至少需要购买甲种原料8千克.
(2)购买甲种原料需9x元,购买乙种原料需5(20-x)元,
则y=9x+5(20-x)=4x+100(8≤x≤20),
y随x增大而增大,
所以当x=8时,y最小,最小费用为132元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2m=5,2n=8,则2m+n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m、n、p都是整数,且|m﹣n|+|p﹣m|=1,则p﹣n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
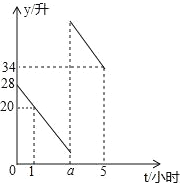
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算和解方程
(1)
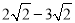 (2)
(2)
(3)
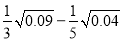 ; (4)
; (4)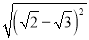
(5)
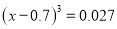 . (6)(2x-3)2=36
. (6)(2x-3)2=36 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.

(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣5和﹣7互为相反数,求a的值.
相关试题

