【题目】问题背景:
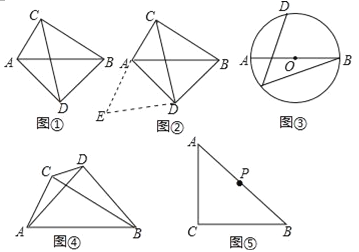
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图①中,若AC=![]() ,BC=
,BC=![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上,![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
参考答案:
【答案】(1)3;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() PQ=
PQ=![]() AC或
AC或![]() PQ=
PQ=![]() AC.
AC.
【解析】
试题分析:(1)由题意可知:AC+BC=![]() CD,所以将AC与BC的长度代入即可得出CD的长度;
CD,所以将AC与BC的长度代入即可得出CD的长度;
(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;
(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1,由(2)问题可知:AC+BC=![]() CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;
CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;
(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.
试题解析:(1)由题意知:AC+BC=![]() CD,∴
CD,∴![]() =
=![]() CD,∴CD=3,;
CD,∴CD=3,;
(2)连接AC、BD、AD,∵AB是⊙O的直径,∴∠ADB=∠ACB=90°,∵![]() ,∴AD=BD,将△BCD绕点D,逆时针旋转90°到△AED处,如图③,∴∠EAD=∠DBC,∵∠DBC+∠DAC=180°,∴∠EAD+∠DAC=180°,∴E、A、C三点共线,∵AB=13,BC=12,∴由勾股定理可求得:AC=5,∵BC=AE,∴CE=AE+AC=17,∵∠EDA=∠CDB,∴∠EDA+∠ADC=∠CDB+∠ADC,即∠EDC=∠ADB=90°,∵CD=ED,∴△EDC是等腰直角三角形,∴CE=
,∴AD=BD,将△BCD绕点D,逆时针旋转90°到△AED处,如图③,∴∠EAD=∠DBC,∵∠DBC+∠DAC=180°,∴∠EAD+∠DAC=180°,∴E、A、C三点共线,∵AB=13,BC=12,∴由勾股定理可求得:AC=5,∵BC=AE,∴CE=AE+AC=17,∵∠EDA=∠CDB,∴∠EDA+∠ADC=∠CDB+∠ADC,即∠EDC=∠ADB=90°,∵CD=ED,∴△EDC是等腰直角三角形,∴CE=![]() CD,∴CD=
CD,∴CD=![]() ;
;
(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1,连接D1A,D1B,D1C,如图④
由(2)的证明过程可知:AC+BC=![]() D1C,∴D1C=
D1C,∴D1C=![]() ,又∵D1D是⊙O的直径,∴∠DCD1=90°,∵AC=m,BC=n,∴由勾股定理可求得:
,又∵D1D是⊙O的直径,∴∠DCD1=90°,∵AC=m,BC=n,∴由勾股定理可求得:![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() =
=![]() =
=![]() ,∵m<n,∴CD=
,∵m<n,∴CD=![]() ;
;
(3)当点E在直线AC的左侧时,如图⑤,连接CQ,PC,∵AC=BC,∠ACB=90°,点P是AB的中点,∴AP=CP,∠APC=90°,又∵CA=CE,点Q是AE的中点,∴∠CQA=90°,设AC=a,∵AE=![]() AC,∴AE=
AC,∴AE=![]() a,∴AQ=
a,∴AQ=![]() AE=
AE=![]() ,由勾股定理可求得:CQ=
,由勾股定理可求得:CQ=![]() a,由(2)的证明过程可知:AQ+CQ=
a,由(2)的证明过程可知:AQ+CQ=![]() PQ,∴
PQ,∴![]() PQ=
PQ=![]() a,∴
a,∴![]() PQ=
PQ=![]() AC;
AC;
当点E在直线AC的右侧时,如图⑥,连接CQ、CP,同理可知:∠AQC=∠APC=90°,设AC=a,∴AQ=![]() AE=
AE=![]() ,由勾股定理可求得:CQ=
,由勾股定理可求得:CQ=![]() a,由(3)的结论可知:PQ=
a,由(3)的结论可知:PQ=![]() (CQ﹣AQ),∴
(CQ﹣AQ),∴![]() PQ=
PQ=![]() AC.
AC.
综上所述,线段PQ与AC的数量关系是![]() PQ=
PQ=![]() AC或
AC或![]() PQ=
PQ=![]() AC.
AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两名同学在调查时使用下面两种提问方式,你认为哪一种更好些( )
A. 难道你不认为科幻片比武打片更有意思吗?
B. 你更喜欢哪一类电影 ——科幻片还是武打片?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两组数据:a1,a2,a3,a4,a5和a1-1,a2-1,a3-1,a4-1,a5-1,下列判断中错误的是( )
A. 平均数不相等,方差相等 B. 中位数不相等,标准差相等
C. 平均数相等,标准差不相等 D. 中位数不相等,方差相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动﹣旋转变换
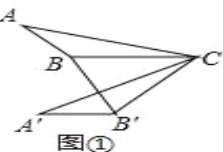
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
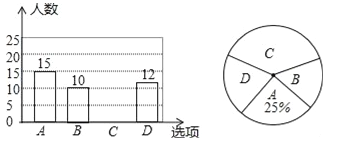
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
-
科目: 来源: 题型:
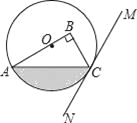
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表: 频数分布表
身高分组
频数
百分比
x<155
5
10%
155≤x<160
a
20%
160≤x<165
15
30%
165≤x<170
14
b
x≥170
6
12%
总计
100%
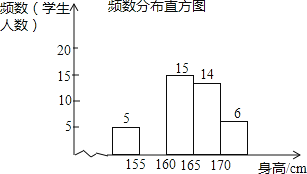
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
相关试题

