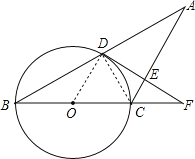
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.

求证:
(1)AD=BD;
(2)DF是⊙O的切线.
参考答案:
【答案】见解析
【解析】
试题分析:(1)由于AC=AB,如果连接CD,那么只要证明出CD⊥AB,根据等腰三角形三线合一的特点,我们就可以得出AD=BD,由于BC是圆的直径,那么CD⊥AB,由此可证得.
(2)连接OD,再证明OD⊥DE即可.
证明:(1)连接CD,
∵BC为⊙O的直径,
∴CD⊥AB.
∵AC=BC,
∴AD=BD.
(2)连接OD;
∵AD=BD,OB=OC,
∴OD是△BCA的中位线,
∴OD∥AC.
∵DE⊥AC,
∴DF⊥OD.
∵OD为半径,
∴DF是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化商场同时卖出两台电子琴,每台均卖960元.以成本计算,第一台盈利20%,另一台亏本20%.则本次出售中,商场( )
A.不赚不赔
B.赚160元
C.赚80元
D.赔80元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M 到x 轴的距离为 7,到y 轴的距离为 2,则点M 的坐标为( )
A. (7,2) B. (-7,-2)
C. (7,-2) D. (2,7)或(2,-7)或(-2,7)或(-2,-7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
63
124
178
302
481
599
1803
摸到白球的频率

0.63
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某医院各部门的示意图,横向表示的是楼层,纵向表示的是门号,例如:院长室在4楼3门,我们用(4,3)来表示其位置,试根据上面方法,结合图形,完成下面问题:

(1)儿科诊室可以表示为 ;
(2)口腔科诊室在 楼 门;
(3)图形中显示,与院长室同楼层的有 ;
(4)与神经科诊室同楼层的有 ;
(5)表示为(1,2)的诊室是 ;
(6)表示为(3,5)的诊室是 ;
(7)3楼7门的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=
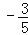 x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.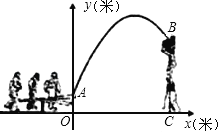
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
相关试题

