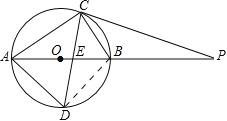
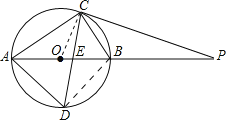
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
参考答案:
【答案】(1)AC=8,AD=5![]() cm;(2)直线PC与⊙O相切,理由见解析.
cm;(2)直线PC与⊙O相切,理由见解析.
【解析】试题分析:(1)、连接BD,根据AB为直径,则∠ACB=∠ADB=90°,根据Rt△ABC的勾股定理求出AC的长度,根据CD平分∠ACB得出Rt△ABD是等腰直角三角形,从而得出AD的长度;(2)、连接OC,根据OA=OC得出∠CAO=∠OCA,根据PC=PE得出∠PCE=∠PEC,然后结合CD平分∠ACB得出∠ACE=∠ECB,从而得出∠PCB=∠ACO,根据∠ACB=90°得出∠OCP=90°,从而说明切线.
试题解析:(1)、①如图,连接BD, ∵AB是直径, ∴∠ACB=∠ADB=90°,
在RT△ABC中,AC=![]() =
=![]() =8cm,
=8cm,
②∵CD平分∠ACB, ∴AD=BD,∴Rt△ABD是直角等腰三角形, ∴AD=![]() AB=
AB=![]() ×10=5
×10=5![]() cm;
cm;
(2)、直线PC与⊙O相切,
理由:连接OC, ∵OC=OA,∴∠CAO=∠OCA, ∵PC=PE, ∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE, ∵CD平分∠ACB, ∴∠ACE=∠ECB,∴∠PCB=∠ACO,∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°, OC⊥PC,
∴直线PC与⊙O相切.
-
科目: 来源: 题型:
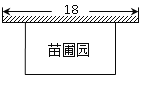
查看答案和解析>>【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的两个平方根分别是3a+2和a+14,则这个正数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

-
科目: 来源: 题型:
查看答案和解析>>【题目】天安门广场的面积约440000平方米. 440000这个数用科学计数法表示为
A. 44×104. B. 4.4×105. C. 0.44×106. D. 4.4×104.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑病毒传播快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.若每轮感染中平均一台电脑会感染x台电脑,则下面所列方程中正确的是( )
A.x(x+1)=81
B.1+x+x2=81
C.(1+x)2=81
D.1+(1+x)2=81
相关试题

