【题目】综合题探究发现
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为;②线段AD,BE之间的数量关系为 . 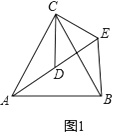
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.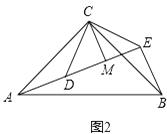
参考答案:
【答案】
(1)∠AEB=60°,AD=BE
(2)解:∠AEB=90°,AE=BE+2CM,
理由:如图2,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
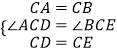 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A、D、E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM,
∴AE=AD+DE=BE+2CM.
【解析】(1)利用等边三角形的性质可证出△ACD≌△BCE,进而得出∠ADC=∠BEC=120°;(2)借鉴(1)的方法,证△ACD≌△BCE,可得出AD=BE,∠ADC=∠BEC,进而得出AE=AD+DE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
为了迎接春运高峰,铁路部门日前开始调整列车运行图,2015年春运将迎来“高铁时代”.甲、乙两个城市的火车站相距1280千米,加开高铁后,从甲站到乙站的运行时间缩短了11小时,大大方便了人们出行.已知高铁行使速度是原来火车速度的3.2倍,求高铁的行驶速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算-(-2x3y4)4的结果是( )
A. 16x12y16 B. -16x12y16
C. 16x7y8 D. -16x7y8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形
 中,
中,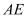 平分
平分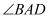 交边
交边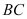 于
于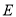 ,
,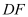 平分
平分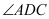 交边
交边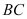 于
于 .若
.若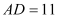 ,
,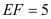 ,则
,则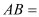 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,是关于x的一元二次方程的是( )
A.5x+5=2x﹣1B.y2﹣7y=0
C.ax2+bc+c=0D.2x2+2x=x2-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】粗心的小红在计算n边形的内角和时,少加了一个内角,求得的内角和是2040°,则这个多边形的边数n和这个内角分别是( )
A.11和60°
B.11和120°
C.12和60°
D.14和120° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查适合采用抽样调查的是( )
A.检查一枚用于发射卫星的运载火箭的各零部件
B.了解全班同学身高状况
C.检查一批灯泡的使用寿命
D.奥运会上对参赛运动员进行的尿样检查
相关试题

