【题目】如图,平行四边形ABCD中,D点在抛物线y= ![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= ![]() ,M是抛物线与y轴的交点.
,M是抛物线与y轴的交点.
(1)求直线AC和抛物线的解析式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动.问:当P运动到何处时,△APQ是直角三角形?
(3)在(2)中当P运动到某处时,四边形PDCQ的面积最小,求此时△CMQ的面积.
参考答案:
【答案】
(1)
解:如图1,∵tan∠ACB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴设AO=3x,CO=4x,∵OB=OC,
∴BO=4x,
∴AB2=AO2+BO2,
则25=25x2,
解得:x=1(负数舍去),
∴AO=3,BO=CO=4,
∴A(0,3),B(﹣4,0),C(4,0),
∴设直线AC的解析式为:y=kx+d,
则 ![]() ,
,
解得:  ,
,
故直线AC的解析式为:y=﹣ ![]() x+3;
x+3;
∵四边形ABCD是平行四边形,
∴BC=AD=8,
∴D(8,3),
∵B,D点都在抛物线y= ![]() x2+bx+c上,
x2+bx+c上,
∴  ,
,
解得:  ,
,
故此抛物线解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣3
x﹣3

(2)
解:①如图2,∵OA=3,OB=4,

∴AC=5.
设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,
∵PQ⊥AC,
∴∠AQP=∠AOC=90°,∠PAQ=∠ACO,
∴△APQ∽△CAO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .
.
②如图3,

设点P运动了t秒时,当QP⊥AD,此时AP=t,CQ=t,AQ=5﹣t,
∵QP⊥AD,
∴∠APQ=∠AOC=90°,∠PAQ=∠ACO,
∴△AQP∽△CAO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .
.
即当点P运动到距离A点 ![]() 或
或 ![]() 个单位长度处,△APQ是直角三角形
个单位长度处,△APQ是直角三角形
(3)
解:如图4,∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD= ![]() ×8×3=12,
×8×3=12,
∴当△APQ的面积最大时,四边形PDCQ的面积最小,
当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,
由△AQH∽△CAO可得: ![]() =
= ![]() ,
,
解得:h= ![]() (5﹣t),
(5﹣t),
∴S△APQ= ![]() t×
t× ![]() (5﹣t)=
(5﹣t)= ![]() (﹣t2+5t)=﹣
(﹣t2+5t)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,S△APQ达到最大值
时,S△APQ达到最大值 ![]() ,此时S四边形PDCQ=12﹣
,此时S四边形PDCQ=12﹣ ![]() =
= ![]() ,
,
故当点P运动到距离点A, ![]() 个单位处时,四边形PDCQ面积最小,
个单位处时,四边形PDCQ面积最小,
则AQ=QC= ![]() ,
,
故△CMQ的面积为: ![]() S△AMC=
S△AMC= ![]() ×
× ![]() ×4×6=6.
×4×6=6.

【解析】(1)首先利用锐角三角函数关系得出A,C点坐标,再求出一次函数解析式,根据平行四边形的性性质求出点D坐标,利用待定系数法可求出b、c的值,继而得出二次函数表达式;(2)设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,再由△APQ∽△CAO或△AQP∽△CAO,利用对应边成比例可求出t的值,继而确定点P的位置;(3)只需使△APQ的面积最大,就能满足四边形PDCQ的面积最小,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽△CAO,利用对应边成比例得出h的表达式,继而表示出△APQ的面积表达式,即可得出四边形PDCQ的最小值,也可确定点P的位置,进而得出Q的位置,进而得出△CMQ的面积.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.

根据上述信息,解答下列问题:
(1)本次抽取的学生人数是;扇形统计图中的圆心角α等于;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定位多少元时,每个月可获得最大利润?最大的月利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
①求证:DC为⊙O切线;
②若ADOC=8,求⊙O半径r.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )

A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴,直线y=﹣x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为( )
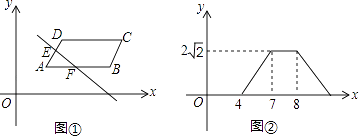
A.4
B.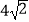
C.8
D.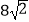
相关试题

