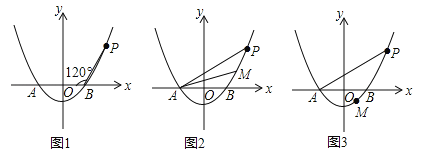
【题目】已知抛物线![]() (a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
参考答案:
【答案】(1)![]() ;(2)①存在,M(3,
;(2)①存在,M(3,![]() );②M(
);②M(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
【解析】
试题分析:(1)先求出A、B两点坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;
(2)①过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、M的坐标,然后代入△APM的面积公式![]() DMAC,根据题意列出方程求出m的值;
DMAC,根据题意列出方程求出m的值;
②根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
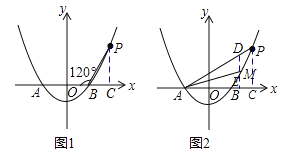
试题解析:(1)如图1,令y=0代入![]() ,∴
,∴![]() ,∵a>0,∴
,∵a>0,∴![]() ,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=
,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=![]() ,∴BC=2,由勾股定理可求得:PC=
,∴BC=2,由勾股定理可求得:PC=![]() ,∵OC=OC+BC=4,∴P(4,
,∵OC=OC+BC=4,∴P(4,![]() ),把P(4,
),把P(4,![]() )代入
)代入![]() ,∴
,∴![]() =16a﹣4a,∴a=
=16a﹣4a,∴a=![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ;
;
(2)∵点M在抛物线上,∴![]() ,∴M的坐标为(m,
,∴M的坐标为(m,![]() );
);
①当点M在曲线PB之间(含端点)移动时,∴2≤m≤4,如图2,过点M作ME⊥x轴于点E,交AP于点D,设直线AP的解析式为y=kx+b,把A(﹣2,0)与P(4,![]() )代入y=kx+b,得:
)代入y=kx+b,得: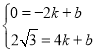 ,解得:
,解得: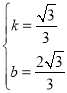 ,∴直线AP的解析式为:
,∴直线AP的解析式为:![]() ,令x=m代入
,令x=m代入![]() ,∴
,∴![]() ,∴D的坐标为(m,
,∴D的坐标为(m,![]() ),∴DM=
),∴DM=![]() =
=![]() ,∴S△APM=
,∴S△APM=![]() DMAE+
DMAE+![]() DMCE
DMCE
=![]() DM(AE+CE)=
DM(AE+CE)=![]() DMAC=
DMAC=![]() ,当S△APM=
,当S△APM=![]() 时,∴
时,∴![]() =
=![]() ,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,
,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,![]() );
);
②当点M在曲线BA之间(含端点)移动时,∴﹣2≤m≤2,n<0,当﹣2≤m≤0时,∴|m|+|n|=﹣m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),当0<m≤2时,∴|m|+|n|=m﹣n=
),当0<m≤2时,∴|m|+|n|=m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(
),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )
A.a≥1
B.a>1且a≠5
C.a≥1且a≠5
D.a≠5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2
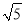 ,AC=2,求四边形AODE的周长.
,AC=2,求四边形AODE的周长.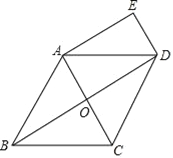
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价是110元,售价是132元,那么这种商品的利润率是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
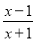 ,
, 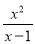 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 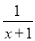 ,
, 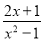 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 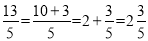 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
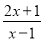 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
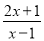 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
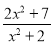 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
-
科目: 来源: 题型:
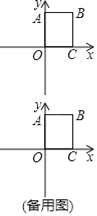
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.
相关试题

