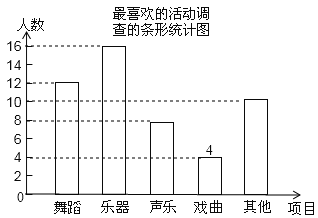
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图。

请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生。其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 。扇形统计图中喜欢“戏曲”部分扇形的圆心角为 度。
(2)请你补全条形统计图。
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率。
参考答案:
【答案】(1)50,24%,28.8°;(2)详见解析;(3)![]() .
.
【解析】
试题分析:(1)用喜欢声乐的人数除以所占的百分比,进行计算即可得出一共抽查了的学生人数;喜欢“舞蹈”活动项目的人数除以被调查的总人数即可;先求出喜欢“戏曲”部分的百分比,再根据扇形所对圆心角的度数与百分比的关系是:圆心角的度数=百分比×360°,即可得出答案;(2)求出喜欢“戏曲”的人数,然后补全统计图即可;(3)列表或画出树状图,然后根据概率公式列式进行计算即可.
试题解析:(1)8÷16%=50,
![]() ×100%=24%,
×100%=24%,
100%-![]() ×100%-
×100%-![]() ×100%―16%―
×100%―16%―![]() ×100%=100%-24%-32%-16%-20%=8%
×100%=100%-24%-32%-16%-20%=8%
喜欢“戏曲”部分扇形的圆心角的度数=8%×360°=28.8°;
(2)补全条形统计图如图
(3)图表或树状图正确
画树状图如下:
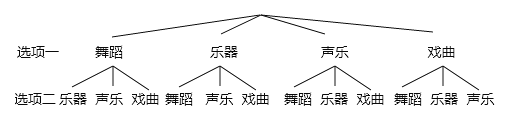
共有12种情况,其中恰好选中“舞蹈、声乐”这两项活动的有2种结果,
故恰好选中“舞蹈、声乐”这两项活动的概率是:![]() =
=![]() .
.
用列表法如下:
舞蹈 | 乐器 | 声乐 | 戏曲 | |
舞蹈 | (舞蹈、乐器) | (舞蹈、声乐) | (舞蹈、戏曲) | |
乐器 | (乐器、舞蹈) | (乐器、声乐) | (乐器、戏曲) | |
声乐 | (声乐、舞蹈) | (声乐、乐器) | (声乐、戏曲) | |
戏曲 | (戏曲、舞蹈) | (戏曲、乐器) | (戏曲、声乐) |
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a2)3a5的运算结果正确的是( )
A.a13
B.a11
C.a21
D.a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+t)(x+6)的积中不含有x的一次项,则t的值是()
A. 0 B. 6 C. -6 D. 6或-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-2+3=( )
A. 1 B. -1 C. 5 D. -5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
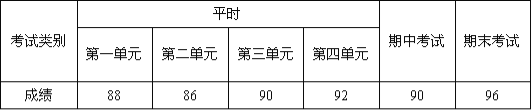
(1)李刚同学6次成绩的极差是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
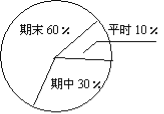
(4)如果用右图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式(a+1)x>a+1的解集是x<1,则a必满足( )
A. a<-1 B. a>-1 C. a<1 D. a>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标为( )
A. (3,1) B. (2,-1) C. (4,1) D. (3,2)
相关试题

