【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题: 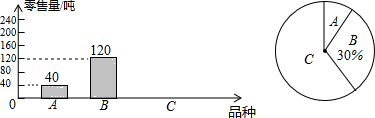
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数;
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
参考答案:
【答案】
(1)解:120÷30%=400(吨)
(2)解:C品种的零售量为400﹣40﹣120=240(吨),
图2中A所在扇形的圆心角的度数为 ![]() ×360°=36°,
×360°=36°,
补全图象如下:

(3)解:300× ![]() =180(千克)
=180(千克)
【解析】(1)根据B品种有120吨,占30%即可求得调查的这三种荔枝的总吨数;(2)根据各品种质量之和等于400可得C品种质量,再用A所占比例乘以360度可得答案;(3)总数量300乘以C品种荔枝的吨数所占的百分比即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).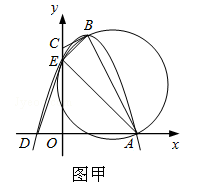
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为 .
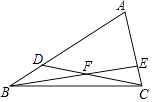
-
科目: 来源: 题型:
查看答案和解析>>【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买
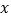 个文具盒,10件奖品共需
个文具盒,10件奖品共需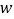 元,求
元,求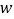 与
与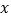 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
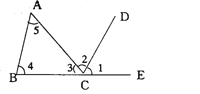
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
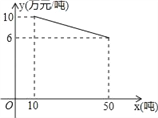
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+4的图象与反比例函数y=
 (k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点.
(k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点.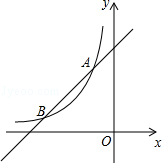
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积.
相关试题

