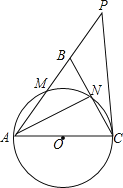
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
参考答案:
【答案】(1)25°;(2)4
【解析】试题分析:(1)根据CP是⊙O的切线,AC为直径,可得∠ACP=90°,再由∠P=40°从而可得∠BAC=50°,再根据AB=AC求得∠ABC的度数即可得;
(2)作BF⊥AC于F,由题意可得∠ANC=90°,再根据等腰三角形的性质求得CN长,再根据直角三角形两锐角互余推得∠BCP=∠CAN,由已知即可得sin∠CAN=![]() ,从而可得.
,从而可得.
试题解析:(1)∵CP是⊙O的切线,AC为直径,
∴∠ACP=90°,
又∵∠P=40°,
∴∠BAC=50°,
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BCP =∠ABC-∠P=65°-40°=25°;
(2)如图,作BF⊥AC于F,
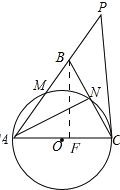
∵AC为直径,
∴∠ANC=90°,
∵AB=AC,
∴CN=![]() CB=
CB=![]() ,
,
∵∠BCP+∠ACN =∠CAN+∠ACN,
∴∠BCP=∠CAN,
∵sin∠BCP=![]() ,
,
∴sin∠CAN=![]() ,
,
∴![]() ,
,
∴AC=5,
-
科目: 来源: 题型:
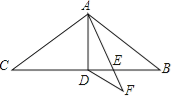
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】厦门市某中学在“六一儿童节”期间举办了七年级学生“数学应用能力比赛”. 为表彩在本次活动中表现优秀的学生,老师决定到某文具店购买笔袋或笔记本作为奖品. 已知1个笔袋和2本笔记本原价共需74元;2个笔袋和3本笔记本原价共需123元.
(1)问每个笔袋、每本笔记本原价各多少元?
(2)时逢“儿童节”,该文具店举行“优惠促销活动,具体办法如下:笔袋“九折”优惠;笔记本不超过10本不优惠,超出10本的部分“八折“优惠. 若老师购买60个奖品(其中笔袋不少于20个)共需
 元,设笔袋为
元,设笔袋为 个,请用含有
个,请用含有 的代数式表示
的代数式表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形
 中,
中, ,点
,点 在
在 边上,
边上, 平分
平分 ,且
,且 .
. 
(1)求证:
 ;
;(2)如图2,已知
 交
交 边于点
边于点 ,交
,交 边的延长线于点
边的延长线于点 ,且
,且 平分
平分 . 若
. 若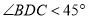 ,试比较
,试比较 与
与 的大小,并说明理由.
的大小,并说明理由. -
科目: 来源: 题型:
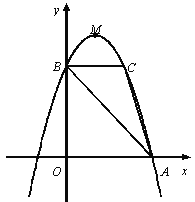
查看答案和解析>>【题目】如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 为坐标原点,将三角形
为坐标原点,将三角形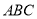 进行平移,平移后点
进行平移,平移后点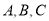 的对应点分别是点
的对应点分别是点 ,点
,点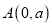 ,点
,点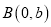 ,点
,点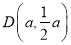 ,点
,点 .
. (1)若
 ,求
,求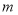 的值;
的值;(2)若点
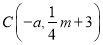 ,其中
,其中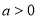 . 直线
. 直线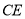 交
交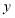 轴于点
轴于点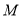 ,且三角形
,且三角形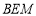 的面积为1,试探究
的面积为1,试探究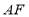 和
和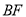 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为( )

A. 36° B. 45° C. 60° D. 72°
相关试题

