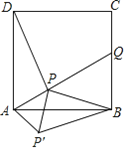
【题目】如图,点P是正方形ABCD内一点,连接AP并延长,交BC于点Q.连接DP.将△ADP绕点A顺时针旋转90°至△ABP'.连结PP',若AP=1,PB=2![]() ,PD=
,PD=![]() ,则正方形的边长为( )
,则正方形的边长为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
参考答案:
【答案】D
【解析】
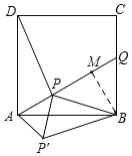
过点B作BM⊥AQ于点M,由折叠的性质可得DP=P'B=2![]() ,AP=AP'=1,∠PAP'=90°,由勾股定理和勾股定理的逆定理可求PP'=
,AP=AP'=1,∠PAP'=90°,由勾股定理和勾股定理的逆定理可求PP'=![]() ,∠APP'=45°,∠BPP'=90°,即可求∠BPM=180°-∠BPP'-∠APP'=45°,由勾股定理可求AB的长.
,∠APP'=45°,∠BPP'=90°,即可求∠BPM=180°-∠BPP'-∠APP'=45°,由勾股定理可求AB的长.
过点B作BM⊥AQ于点M,
∵将△ADP绕点A顺时针旋转90°至△ABP',
∴DP=P'B=2![]() ,AP=AP'=1,∠PAP'=90°,
,AP=AP'=1,∠PAP'=90°,
∴PP'=![]() ,∠APP'=45°,
,∠APP'=45°,
∵P'P2+PB2=2+8=10,P'B2=10,
∴P'P2+PB2=P'B2,
∴∠BPP'=90°,
∴∠BPM=180°-∠BPP'-∠APP'=45°,
∵BM⊥AQ,
∴∠BMP=90°,
∴∠PBM=90°-∠BPQ==45°,PM2+BM2=PB2,
∴∠PBM=∠BPM,
∴PM=BM,
又∵PB=2![]() ,PM2+BM2=PB2,
,PM2+BM2=PB2,
∴PM=BM=2,
∴AM=AP+PM=3,
∴AB=![]() ,
,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B =∠C,点D、E分别是边AB、AC上的点,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延长线于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P与∠A的数量关系,并证明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
-
科目: 来源: 题型:
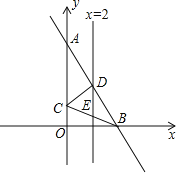
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
(1)求证:∠OCB=2∠CBA;
(2)求点C的坐标和直线BC的解析式;
(3)求△DEB的面积;
(4)在x轴上存在一点P使PD-PC最长,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=
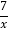 (x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=-
(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=- (x<0)的图象于点E,则图中阴影部分的总面积为______.
(x<0)的图象于点E,则图中阴影部分的总面积为______.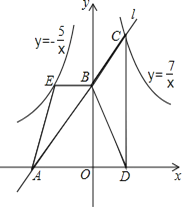
-
科目: 来源: 题型:
查看答案和解析>>【题目】用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系,寄宿生小红和小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水(约10升),小敏每次用半盆水(约5升).如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克.
(1)请帮助小红和小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x之间的函数关系式
(2)当洗衣粉的残留量降至0.5克时,便视为衣服漂洗干净,从节约用水的角度来看,你认为谁的漂洗方法值得提倡?为什么?
相关试题

